
우리의 가장 가까운 별인 태양은 자기장과 상호 작용하는 혈장 공입니다. 이 상호 작용은 매혹적이고 복잡한 역학으로 이어집니다. 태양의 눈에 보이는 노란색 디스크 (육안으로 직접 보지 않아야 함) 자국, 대략 태양 대기의 바닥.
태양의 대기에서는 자기장 (광구를 통해 나타날 수있는)이 불안정해질 때까지 뷔페, 꼬임 및 전단이 발생합니다. 이러한 분화는 그 자체로 흥미로워지는 것 외에도 지구의 인공 위성과 전력망을 방해 할 수있는 우주 날씨의 기초를 형성합니다. 따라서 혈장 불안정성과 분화의 기초를 이해하는 것은 이론적이고 실용적으로 중요합니다.
이 기사는 혈장 물리학의 고전적인 불안정성에 대한 최근의 새로운 통찰력, 즉 찢어짐 불안정성을 요약합니다. 찢어짐 불안정성이 발생하기 위해서는 현재 시트라고하는 영역이 필요하며, 여기서 자기장은 매우 작은 길이 스케일에 따라 방향이 바뀝니다 (그림 1a 참조). 불안정성이 발생하면 자기장은 '눈물', 재 연결 및 자기 섬에서 줄을 긋습니다 (그림 1B). 이 불안정성은 태양 플레어의 점화의 핵심 후보입니다.
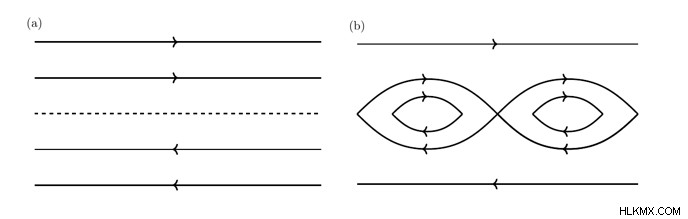
Furth et al. (1963), 찢어짐 불안정성의 시작의 성장 속도는 많은 태양 광 응용에 비해 너무 느린 것으로 간주되었다. 최근 몇 년 동안, 물리학 자들의 새로운 발견은 현재 시트의 폭이 임계 두께에 도달하면 찢어짐 불안정의 빠른 단계를 보여 주었다 (예 :Lourerio et al. 2007, Lapenta 2008, Pucci &Velli 2014).
.수학자의 관점에서 볼 때, 찢어짐 불안정성에 대한 이론적 분석은 지금까지 불안정의 특정 단계에만 초점을 맞추 었습니다. 세부 사항으로 들어 가지 않고 불안정성의 시작을 설명하는 방정식은 '정상'또는 '비정규'로 설명 될 수 있습니다. 정상적인 시스템의 경우, 불안정성의 성장 속도에 해당하는 가장 큰 (측정 방법에 따라) 고유 값 (해당 시스템과 관련된 특성 숫자)을 찾습니다. 이것은 불안정의 시작을 연구하는 고전적인 방법입니다. 비 정상 시스템의 경우 고유 값은 불안정성의 시작에 대한 완전한 설명을 제공하지 않습니다. 대신, 그들은 큰 시간 척도에서 행동을 설명하고 초기에 상당한 일시적 성장 가능성을 설명하지 않습니다.
찢어짐 불안정성을 설명하는 데 사용되는 기본 (여전히 복잡하지만)은 유체 역학의 결합 (플라즈마는 전기적으로 전도성 유체로 취급됨) 및 Magnetohydrodynamics (MHD)로 알려진 전자기를 나타냅니다. 찢어짐 불안정성의 시작을 설명하는 MHD 방정식은 비 정상입니다. 따라서 이러한 방정식에 대한 솔루션은 큰 일시적 에너지 성장을 보여줄 가능성이 있습니다. 그러한 일시적인 성장이 존재한다면, 시스템의 고유 값 만 고려하여 예측 된 것보다 더 빠른 역학으로 이어질 수 있습니다.
.비 정상 시스템이 반드시 큰 일시적 에너지 성장을 생성하는 것은 아닙니다. 또 다른 중요한 요소는 현재 시트에 부과되는 초기 섭동의 형태입니다. 최대 효과를 보여주기 위해 모든 유형의 초기 섭동에 최적화 된 최적의 에너지 성장을 계산할 수 있습니다. 그림 2는 특정 매개 변수 세트에 대한 찢어짐 불안정성의 시작을위한 최적의 에너지 성장의 예를 제공합니다.
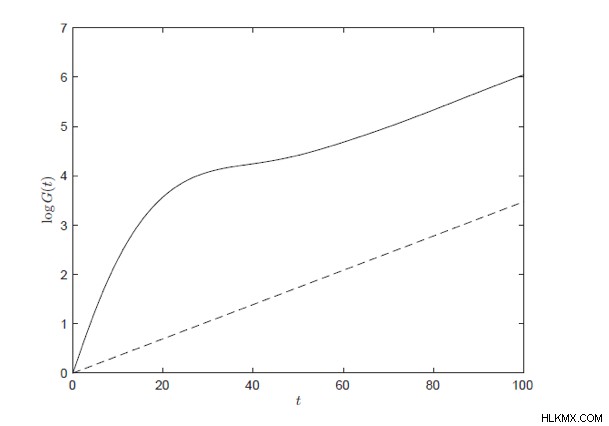
점선은 가장 큰 고유 값 만 고려할 때 최적의 에너지 성장을 나타냅니다 (전형적인 분석). 실선은 고전 이론을 넘어서 시스템의 비정규 효과를 포함 할 때 최적의 에너지 성장을 보여줍니다. 초기에, 일시적 성장은 고전 이론에 의해 예측 된 것보다 훨씬 더 많은 에너지 성장 (주어진 시간 내에)을 매우 빠르게 증가시킵니다. 나중에, 일시적 동작이 이제 쇠퇴하고 솔루션이 가장 큰 고유 값에 의해 지배함에 따라 고체와 점선이 평행 해집니다.
.이러한 유형의 분석은 최근에만 태양 분위기에만 적용되었으며 이전 분석이 감지 할 수없는 더 빠른 에너지 성장을 발견하여 태양에 대한 불안정성과 분화에 대한 이해를 크게 향상시킬 수있는 잠재력을 가지고 있습니다.
.참조 :
- 시트 핀치의 유한 저항성 불안정 (1963) Furth, H.P., Kileen, J., Rosenbluth, M.N., Phys. 유체, 6, 459.
- 거시적 스케일 (2008), Lapenta, G., Phys. Lett., 100, 235001.
- 전류 시트의 불안정성 및 플라스 이드 사슬의 형성 (2007), Lourerio, N.F., Schekochihin, A.A., Cowley, S.C., Phys. 플라즈마, 14, 100703.
- 준-싱글 큘러 전류 시트의 재 연결 :"이상적인"찢어짐 모드 (2014) Pucci, F., Velli, M., Astrophys. J. Lett., 780, L19.
- 비정규 시스템의 수학에 대한 자세한 내용은 독자가 논문으로 향합니다.
- Spectra and Pseudospctra (2005), Trefethen, L.N. &Embree, M., Princeton University Press
이러한 결과는 Solar Physics 저널에 발표 된 현재 시트의 최적 에너지 성장이라는 제목의 기사에 설명되어 있습니다. 이 작품은 글래스고 대학교에서 David Mactaggart가 주도했습니다.







