Celestial Mechanics는 수학과 물리학의 교차점에서 지점으로, 주요 목표는 질량 또는 전하와 같은 일부 물리적 특성과 특정 기하학적 형태를 특징으로하는 수의 신체 (3 차원 공간)의 움직임을 설명하는 것입니다. 이 모든 것은 일반적으로 입자 시스템이라고합니다.
입자 시스템으로 작업을 시작하기 위해, 일단 관련된 신체의 기하학과 특성이 확립되면, 다음 단계는 신체의 상호 작용 법칙을 나타내는 수학적 기능을 정확하며, 이는 잠재적 기능이라고합니다. 이 시점에서, 위치, 속도 및 가속도를 포함하는 방정식 시스템이 얻어진다. 위의 모든 것이 그러한 문제를 공격하는 데 관심이있는 사람은기도를 시작해야 할 수도 있습니다…
천상의 역학에 대한보다 평범한 상황 연구는 N-body 문제로 알려져 있습니다. 여기서 n 포인트 질량, 즉 신체는 완벽하게 구형적이고 질량을 단일 물리적 특성으로, m 1 로 표시합니다. ,…, m n D 차원 유클리드 공간에서 이동하지만, 우리는 사례에 가장 관심이 있지만 d =2 및 3. 대중의 위치가 x 1 로 작성된 경우 , x 2 ,…, x n ,
그리고 우리는 r ij 를 보자 =ix i - - x j 질량 i 사이의 거리를 나타냅니다 및 j . 신체 간의 상호 작용은 뉴턴의 잠재력에 의해 주어집니다 :
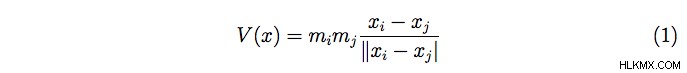
그런 다음 방정식은 다음과 같습니다.
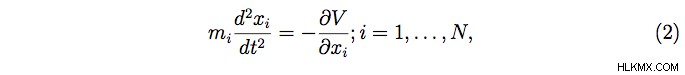
식 (2)는 일반적으로 n 이라고합니다 -몸 방정식, 뉴턴 방정식 또는 n -몸 문제 (Meyer et al., 2009). n 의 역사 -신체 문제는 뉴턴에서 포인 케어에 이르기까지 가장 화려한 마음 중 일부에서 거의 3 세기의 기여를했습니다. 그러나 이것은이 문제의 가장 매혹적인 특징이 아닙니다.
결국, 식 (2)는 n =1 에 대해서만 해결되었습니다. 및 n =2 , 그러나 n -몸 문제는 3 개 이상의 신체를 고려할 때 열린 문제입니다. 천상의 역학에 유혹 된 사람은 공간에서 3 개의 물체가 움직이는 세 가지의 구성, 예를 들어 별 3 개 또는 별, 행성 및 위성 또는 헬륨 원자의 핵과 함께 두 전자와 함께 핵의 핵을 상상하기 시작할 수 있습니다. 앞에서 말했듯이,이 지점의 공간 위치는 3 개의 벡터 x 1 로 표시됩니다. , x 2 , x 3 , 그리고 물체의 질량은 m 1 로 표시됩니다. , m 2 , m 3 . 대중은 그들의 위치 x i 를 도와줍니다 시간 t 의 함수입니다 .
이러한 조건에서 식 (2)는 다음과 같이 재 작성됩니다
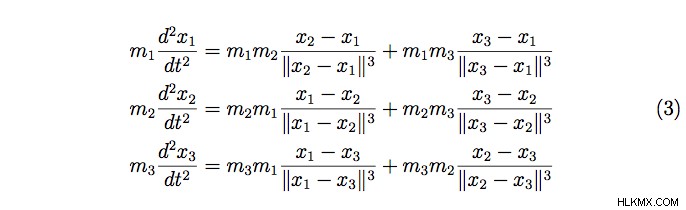오른쪽은 매우 유명한 물리적 상수, 뉴턴의 보편적 인 상수, . 그러나 수학에서는 구조를 통해 우리는 g 을 설정할 수있었습니다. =1. n 의 경우 =1 및 n =2 간단한 미적분 도구를 사용하여 신체의 궤적은 일종의 원뿔이어야한다는 것을 증명했지만 n =3, 가능한 모든 궤적은 무엇입니까?
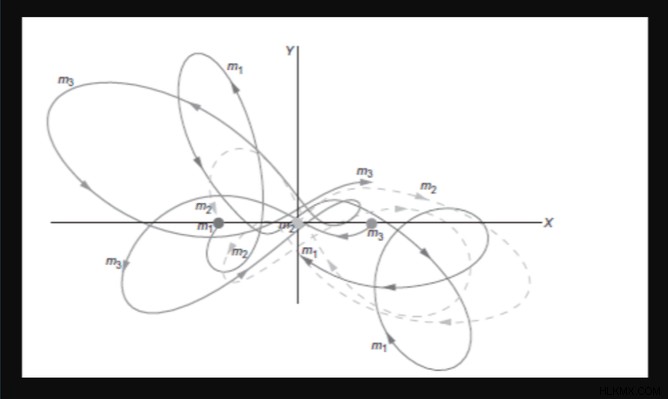
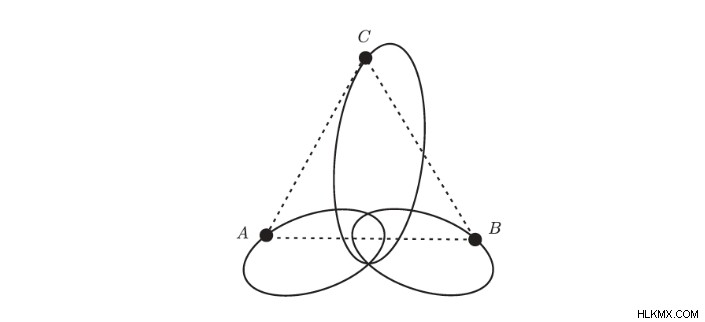
이전 질문은 너무 어렵 기 때문에 특정 상황에 대한 답을 얻는 것이 가능했습니다. 질량, 신체의 특정 구성 등과 같습니다. 이러한 특수 구성 중 하나는 Euler와 Lagrange에 의해 확립되었으며“상대 평형의 문제”라고 불립니다. 이는 회전 시스템에서 평형 상태를 유지하는 신체의 구성 또는 위치 및 가속도 벡터가 비례하는 구성과 동일한 비례와 비례하는 구성입니다.
.이 특별한 문제는 일반 n 과 어색함이 비슷합니다. -몸매는 여전히 n 에 열려 있습니다 ≥ 6. 그러나 이러한 구성의 여러 응용, 특히 공간 여행을위한 궤적 설계에서 Steve Smale은 21 세기에 해결해야 할 문제 목록에 포함하도록 모호했습니다 (Smale, 2000). 이 목록에서 여섯 번째 문제가 언급 한 바와 같이, 우리는 천상의 역학에서 상대 평형 수의 유한성을 증명해야합니다.
상대 평형을 찾거나보다 일반적으로 n 에 대한 결과를 찾으려면 -몸 문제는 수학적 관심사 일뿐 만 아니라 응용 프로그램에서도 매우 중요합니다. 따라서 입자 시스템에 대한 설명은 가능한 한 정확해야하지만 식 (1)의 잠재적 기능은 구형 몸체에만 작용합니다. 더욱이, 우리는 고전 역학의 방정식이 예를 들어 수은의 지위 전달과 같은 행동을 설명하지 못한다는 것을 알고있다. 그래서 우리는 무엇을 할 수 있습니까? 두 가지 질문이 나타납니다.
1. 지구와 행성이 일반적으로 지구를 공전하는 위성을 모델링하는 방법 (예 :지구와 행성은 완벽하게 구형적인 물체와는 거리가 멀다.
2. Newtonian 역학을 일반화하는 물리적 이론은 일반적인 상대성입니다. 그런 다음 행성 시스템의 역학과 퀘이사, 은하 및 블랙홀과 같은 대상에 대한 더 나은 설명을 달성하기 위해 이것을 사용해 보지 않겠습니까?
첫 번째 질문에 대한 답은 모든 특정 문제에 대한 잠재적 기능을 찾아야합니다. 이것은 부분적 미분 방정식에서 어려운 문제인 포아송 방정식을 해결함으로써 이루어지며, 가장 간단한 잠재적 기능은 구형 몸 사이의 상호 작용에 대한 것입니다 (Arredondo et al., 2012).
.두 번째 질문의 경우, Newtonian Mechanics와 달리 일반적으로 상대성 이론에서도 2- 바디 문제의 가장 간단한 경우조차 해결할 수 없습니다.
.위에서 설명한 장애물을 극복하는 방법은 문제에 대한 지속적이고 고전적인 설명을 찾는 것입니다. 그러나 실험적 관찰과 일치하는 잠재적 기능 :잠재적 인 기능입니다. 이렇게하면 n 을 얻습니다 -신체 사이의 상호 작용이 형태의 잠재력으로 설명되는 신체 문제 :
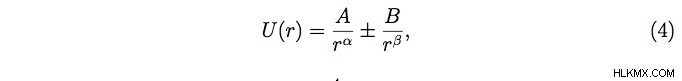
여기서 r 신체 사이의 거리, a, b, α 입니다 및 β 양의 상수입니다. 이러한 종류의 잠재력을 준 유전자라고합니다. 발현 (4)은 Birkhoff, Manev, Van der Waals, Libhoff, Schwarzschild, Lennard-Jones, The Classical Newton 및 Coulomb과 같은 생물학, 천체 물리학 또는 화학의 문제를 모델링하는 잘 알려진 몇 가지 준 유전성 잠재력을 일반화합니다 (Sthephani et al., 2003 참조).
케플러 문제조차도 분석적 솔루션이 없기 때문에 식 (2)은 이러한 잠재력을 사용하여 뉴턴의 잠재력보다 더 어려워집니다. 이 모든 것이 우리는 도구가 답을 얻을 수 있도록 훨씬 더 깊이 보이게합니다. 이 검색은 매우 가시적인 길이지만 보상은 놀랍습니다.
이러한 결과는 최근 저널 Advances in Space Research 에 출판 된 준 유전자 평면 3- 바디 문제의 상대 평형이라는 제목의 기사에 설명되어있다. . 이 작품은 Fundación Universitaria Konrad Lorenz의 John A. Arredondo가 수행했습니다.
