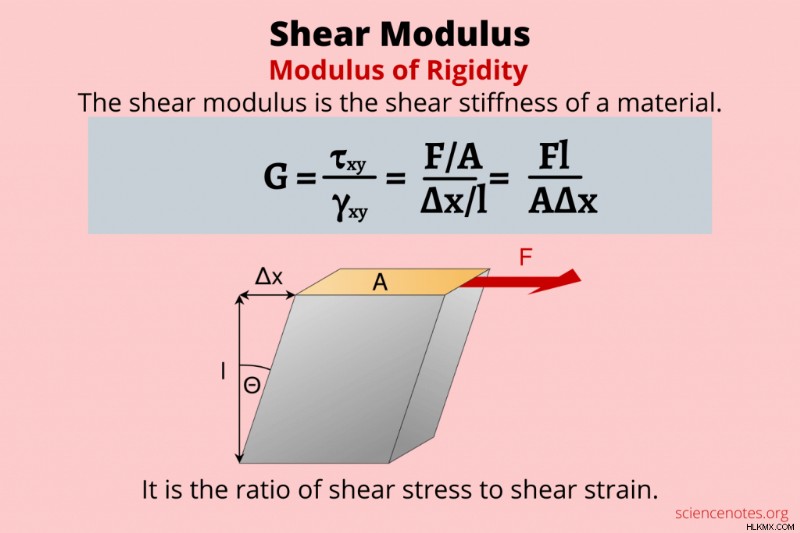
정의상 전단 계수 재료의 전단 강성은 전단 응력 대 전단 변형률의 비율입니다. 전단 계수의 또 다른 이름은 강성 계수입니다. 전단 계수의 가장 일반적인 상징은 대문자 G입니다. 다른 기호는 S 또는 입니다. .
- 높은 전단 계수가있는 재료는 단단한 고체입니다. 변형을 유발하는 데 큰 힘이 필요합니다.
- 전단 계수가 낮은 재료는 부드러운 고체입니다. 힘이 거의 없음으로 변형됩니다.
- 유체의 한 가지 정의는 전단 계수가 0 인 물질이라는 것입니다. 모든 힘은 변형을 유발합니다. 따라서 액체 또는 가스의 전단 계수는 0입니다.
전단 계수 유닛
전단 계수의 SI 단위는 압력 단위 Pascal (PA)입니다. 그러나 파스칼은 제곱 미터당 뉴턴 이므로이 장치도 사용 중입니다. 다른 공통 단위는 GPA (Gigapascal), 제곱 인치당 파운드 (PSI) 및 제곱 인치당 킬로 파운드 (KSI)입니다.
전단 모듈러스 공식
전단 계수 공식은 다른 형태를 취합니다 :
g =τ
- g는 전단 계수 또는 강성의 모듈러스입니다 입니다
- τ
xy 또는 f/a는 전단 응력
입니다 - γ xy 전단 변형입니다
- 전단 변형은 Δx/l =tan θ 또는 때때로 =θ 입니다.
- θ는 적용된 힘의 변형에 의해 형성된 각도입니다
- a는 힘이 작용하는 영역입니다
- Δx는 가로 변위 입니다
- l은 초기 길이 입니다
예제 전단 응력 계산
예를 들어, 4 × 10 N/M의 응력 아래에 있고 5 × 10의 변형이 발생하는 샘플의 전단 계수를 찾으십시오.
.g =τ/γ =(4 × 10 N/M)/(5 × 10) =8 × 10 N/M 또는 8 × 10 PA =800 kPa
등방성 및 이방성 재료
재료는 전단과 관련하여 등방성 또는 이방성입니다. 등방성 물질의 변형은 적용된 힘에 대한 방향이 무엇이든 동일합니다. 대조적으로, 이방성 물질의 스트레스 또는 변형은 방향에 따라 다릅니다.
많은 일반적인 재료는 이방성입니다. 예를 들어, 힘이 결정 격자와 정렬 될 때 다이아몬드 크리스탈 (입방 크리스탈이있는)은 훨씬 더 쉽게 전단됩니다. 목재의 제곱 블록은 목재 곡물에 평행 한 힘을 적용할지 여부에 따라 힘에 다르게 반응합니다. 등방성 재료의 예로는 유리 및 금속이 있습니다.
온도 및 압력에 대한 의존성
온도와 압력은 재료가 적용된 힘에 반응하는 방식에 영향을 미칩니다. 일반적으로 온도를 높이거나 압력 감소는 강성과 전단 계수가 낮아집니다. 예를 들어, 대부분의 금속을 가열하면 작업이 더 쉬워지고 차가워지면 Brittleness가 증가합니다.
전단 계수에 영향을 미치는 다른 요인에는 용융점 및 공석 형성 에너지가 포함됩니다.
기계적 임계 값 응력 (MTS) 플라스틱 흐름 모델, NADAL 및 LEPOAC (NP) 전단 응력 모델 및 Steinberg-Cochran, Guinan (SCG) 전단 응력 모델은 모두 온도 및 압력이 전단 응력에 미치는 영향을 예측합니다. 이 모델은 과학자와 엔지니어가 전단 응력의 변화가 선형 인 온도와 압력 범위를 예측하는 데 도움이됩니다.
전단 계수 값
재료의 전단 계수 값은 온도와 압력에 따라 다릅니다. 다음은 실온에서 대표 물질에 대한 전단 계수 값의 표입니다. 낮은 전단 계수 값은 부드럽고 유연한 재료를 설명하지만 단단하고 뻣뻣한 물질은 전단 계수 값이 높습니다. 예를 들어, 전이 금속, 합금 및 다이아몬드의 전단 계수 값이 높습니다. 고무와 일부 플라스틱은 값이 낮습니다.
| 재료 | Shear Modulus (GPA) |
| 고무 | 0.0006 |
| 폴리 에틸렌 | 0.117 |
| 합판 | 0.62 |
| 나일론 | 4.1 |
| 리드 (PB) | 13.1 |
| 마그네슘 (mg) | 16.5 |
| 카드뮴 (CD) | 19 |
| kevlar | 19 |
| 콘크리트 | 21 |
| 알루미늄 (al) | 25.5 |
| 유리 | 26.2 |
| 황동 | 40 |
| 티타늄 (ti) | 41.1 |
| 구리 (Cu) | 44.7 |
| 철 (Fe) | 52.5 |
| 스틸 | 79.3 |
| 다이아몬드 (C) | 478.0 |







