개념 이해 :
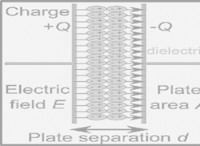
* 대칭 : 무한 전하 시트는 완벽한 대칭을 가지고 있습니다. 시트의 모든 지점은 다른 모든 지점과 동일합니다. 이 대칭은 결과에 중요합니다.
* 가우스의 법칙 : 우리는 가우스의 법칙을 사용하여 전기장을 계산합니다. 이 법은 폐쇄 표면을 통한 전기장의 플럭스가 밀폐 된 전하에 비례한다고 명시하고 있습니다.
* 가우스 표면 선택 : 열쇠는 시트의 대칭을 이용하는 가우스 표면을 선택하는 것입니다. 우리는 시트에 수직으로 축의 원통형 가우시안 표면을 선택합니다. 실린더는 시트로 절반으로 절단되므로 실린더의 절반은 시트의 각 측면에 있습니다.
필드가 일정 한 이유 :
1. 필드 라인 : 대칭으로 인해 전기장 라인은 시트에 수직이며 전하에 따라 시트를 가리키십시오 (또는).
2. 실린더를 통한 플럭스 : 가우스 실린더의 곡선 측면을 통한 전기 플럭스는 전기장 라인이 이들 측면과 평행하기 때문에 0입니다.
3. 끝을 통한 플럭스 : 실린더의 각 끝을 통한 플럭스는 전기장의 크기에 끝 영역을 곱한 것과 같습니다. 필드는 전체 끝에서 일정하므로 각 끝을 통한 플럭스는 동일합니다.
4. 동봉 된 전하 : 가우스 표면으로 둘러싸인 전하의 양은 실린더 끝 영역에 비례합니다.
5. 가우스의 법률 적용 : 가우스의 법칙을 적용하면 끝을 통한 플럭스는 밀폐 된 전하에 비례합니다. 플럭스는 전기장의 면적에 비례하기 때문에, 밀폐 된 전하는 면적에 비례하기 때문에 전기장은 면적과 독립적이며 (따라서 시트로부터의 거리).
결론 :
전기장은 시트의 대칭성과 가우스의 법칙이 표면을 통한 플럭스와 밀폐 된 전하와 관련된 방식으로 인해 무한 전하 시트와의 거리와 무관합니다. 이것은 시트에 수직 인 일정한 전기장을 초래합니다.