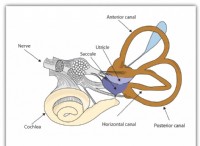
법은 다음과 같습니다.
1. 주파수는 문자열의 길이에 반비례합니다.
- 짧은 문자열은 더 높은 주파수 (높은 피치)에서 진동합니다.
- 문자열의 길이를 두 배로 늘리면 주파수가 절반으로 줄어 듭니다.
2. 주파수는 장력의 제곱근에 비례합니다.
- 문자열의 장력을 높이면 주파수가 높아집니다 (피치가 높아짐).
- 장력을 두 배로 늘리면 주파수가 제곱근의 계수 2 (약 1.414)만큼 증가합니다.
3. 주파수는 단위 길이 당 질량의 제곱근에 반비례합니다 :
- 더 무거운 문자열 (단위 길이 당 질량이 많음)은 낮은 주파수 (낮은 피치)에서 진동합니다.
- 단위 길이 당 질량을 두 배로 늘리면 주파수가 절반이됩니다.
수학적 표현 :
이 법은 다음 공식으로 요약 될 수 있습니다.
f =(1/2l) * √ (t/μ)
어디:
* f 진동 문자열의 기본 주파수입니다
* l 문자열의 길이입니다
* t 문자열의 장력입니다
* μ 문자열의 단위 길이 당 질량입니다
악기에 대한 시사점 :
이 법은 음악가들이 현악기의 피치를 어떻게 바꿀 수 있는지 설명합니다.
* 길이 변경 : 이것은 지판을 따라 다른 지점 (기타와 같은)에서 끈을 아래로 눌러 수행됩니다.
* 장력 변경 : 이것은 피아노와 바이올린과 같은 악기에 페그를 조정하여 수행됩니다.
* 재료 변경 : 다른 재료 (예 :나일론 대 강철)의 줄을 사용하면 단위 길이 당 질량이 변경됩니다.
기본을 넘어서 :
이 법률은 기본 주파수 (문자열에 의해 생성 된 가장 낮은 노트)를 설명하지만, 색조 또는 고조파도 있습니다. 이들은 기본 주파수의 배수 인 주파수로, 문자열의 전체 사운드와 음색에 기여합니다.
진동 현막에 대한 연구는 음향과 음악 이론의 중요한 부분입니다. 사운드가 어떻게 생성되는지와 악기가 다른 피치와 톤을 생성하도록 설계되는 방법을 이해하는 데 도움이됩니다.