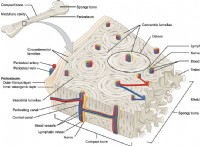
Sharp-Hartman 원칙 분석 분야의 수학적 개념, 특히 함수의 특성에 중점을 둡니다. 수학자 Harold S. Sharp와 Philip Hartman의 이름을 따서 명명되었습니다.
여기에 고장이 있습니다 :
* Sharp : 이 용어는 원리 자체를 설명하는 데 직접 사용되지 않습니다. 진술과 증거에서 원리의 강점이나 정밀도를 강조하는 데 사용될 수 있습니다.
* Hartman : 이것은 Philip Hartman의 발전에 대한 기여를 인정하는 원칙의 이름의 일부입니다.
* 기본 : 이 용어는 분석의 특정 측면을 이해하는 데있어 원리의 중요성과 기본적 역할을 나타내는 데 사용될 수 있습니다.
명확하게하기 위해, 샤프 하트만 원칙은 다음을 나타냅니다.
* 연속 함수와 특정 조건에서 통합이 주어지면 기능은 높은 수준의 정확도와 통합으로부터 재구성 될 수 있습니다. 이것은 본질적으로 함수의 적분을 알고 있다면 Sharp-Hartman 원칙을 사용하여 원래 함수의 근사치를 얻을 수 있음을 의미합니다.
원칙의 이름에는 "확산"이 직접 포함되지 않습니다. 이 개념과 관련하여 "확산"을 만나면 널리 받아 들여지거나 표준화되지 않은 Sharp-Hartman 원칙의 특정 응용 프로그램 또는 해석을 참조 할 수 있습니다.
주목하는 것이 중요합니다 : "날카로운 원리 확산 및 기본"에 대한 구체적인 정보를 찾고 있다면 더 많은 맥락을 제공하는 것이 필수적입니다. 이것은 당신이 만나는 날카로운 하트만 원리의 특정 응용 프로그램 또는 해석을 이해하는 데 도움이 될 것입니다.