연구원들은 많은 별들이 부분이라고 확립했다 배수 - 스타 시스템. 또한, 우리 은하에서 다중 스타 시스템의 비율은 약 3 분의 2 인 것으로 가정합니다. 별을 보면 별은 별이 독방적이고 고립 된 물체라고 믿게 할 수 있지만 실제로는 별이별로 태어나지 않습니다.
항성 시스템은 중력 n 를 적용하여 모델링 할 수 있습니다. -몸 문제. 중앙 구성 (CC)은 중력 n 에서 매우 중요한 장입니다. -대칭 적으로 제한된 4- 및 5 개의 신체 문제의 신체 문제.
n 의 특정 위치 위치와 가속 벡터가 동일한 비례의 상수에 비례하는 경우 CC를 정의합니다.
그들은 운동 방정식과 주기적 솔루션 패밀리의 명백한 동종 솔루션을 제공하는 데 도움이됩니다. 충돌에 가까운 솔루션의 특성을 관찰하고 적분 매니 폴드의 토폴로지에 영향을 미칩니다.
4 점 또는 5 점 질량 모션은 적어도 하나의 대칭 축을 갖는 마름모 또는 삼각형을 형성 할 때 조사되고있다. 대칭 축에 3 개의 콜린 아르가 불평등 한 질량이 있습니다. 나머지 두 질량은 대칭 축 양쪽에 대칭 적으로 위치합니다.
3 가지 사례가 연구되고있다 :첫째, 4 개의 질량이 마름모를 형성하고, 다섯 번째 질량은 대칭 축의 어느 곳에도 배치된다. 둘째, 5 개의 질량은 삼각형을 형성 할 것이다. 셋째, 특별한 경우에, 5 질량을 0과 동일하게함으로써 우리는 또한 4- 바디 구성에 대해 논의합니다.
중앙 구성 영역은 일반적인 문제의 다양한 특별한 경우에 대해 결정하고 있습니다. 마름모의 정점에 두 쌍의 질량이 배치되고 5 덩어리가 대칭 축 (원점 제외)의 어느 곳에도 배치 될 때 중심 구성이 불가능합니다.
무용가 4 및 5 바디 문제에서 이등변 및 평형 삼각 5- 바디 문제 사례 중앙 구성의 영역은 분석 및 수치 기술을 사용하여 도출됩니다.
정규화 된 운동 방정식이 결정되고 있으며, Poincaré 섹션을 통해 위상 공간의 혼란스러운 거동이 조사되고 있습니다. 더욱이주기적이고 준 주변 궤도가있는 지역이 식별되고 있습니다.
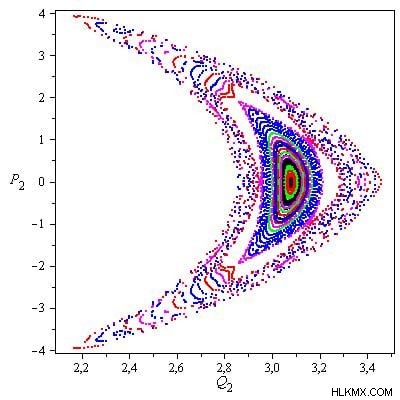
예를 들어, 제 1과 제 3의 질량이 동일 할 때 1 , 두 번째 및 네 번째 몸의 질량은 동일합니다 2 , 다섯 번째 질량은 매우 작습니다. 0 . 04 , 우리는 그림 1에 표시된 섹션의 Poincaré 표면을 얻습니다. 그림 1의 내부 영역은 규칙적인 구조와 일부 준 기공 궤도의 존재를 가리 킵니다. rhomboidal 5-body 문제의 4 개의 비등 한 질량 사례에서, 다섯 번째 몸이 매우 작을 때, 외부 영역은 혼란스러운 행동을 나타냅니다.
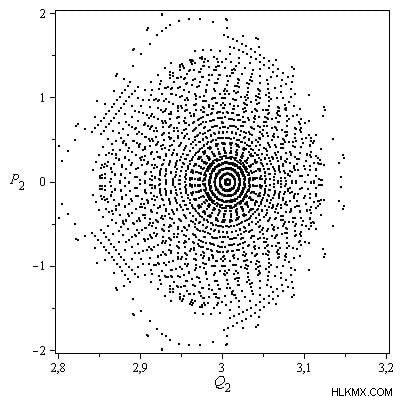
경우, 두 개의 대칭 질량 m 1 인 경우 =m 3 =1.1 그리고 다른 두 대칭 질량 m 2 =m 4 = 1 중앙 질량 3.15, 그림 2에 제시된 섹션의 표면은 원 모양의 준 궤도와 섬 궤도를 포함하여 다양한 유형의 궤도를 보여줍니다.

원형 궤도의 일부에서 변형을 주목하여 근처 섬 궤도의 존재를 나타냅니다. 중앙 몸체가 작을 때, 섹션의 표면은 혼란스러운 영역으로 둘러싸인 준 기공 궤도를 거의 나타냅니다. 중앙 질량의 증가는 문제의 역학을 변화시킵니다 (그림 3 참조)
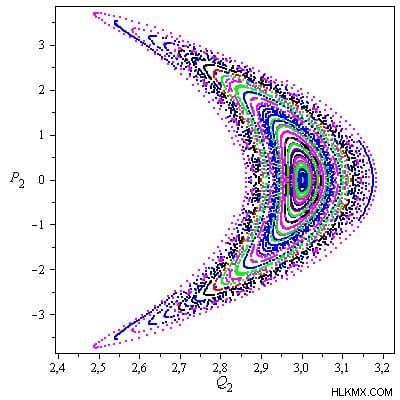
중앙 질량 증가는 Rhomboidal 5-body 구성에 안정화 효과를 갖습니다.
이러한 결과는 Astrophysics and Space Science 저널에 발표 된 Rhomboidal 및 삼각 4 및 5 바디 문제의 평면 중앙 구성에 관한 기사에 설명되어 있습니다. 이 작업은 Muhammad Shoaib (Higher Colleges of Technology), Abdul Rehman Kashif (Capital University of Sciences and Technology) 및 Iharka Szücs-Csillik (루마니아 아카데미의 천문학 연구소)에 의해 주도되었습니다.
.