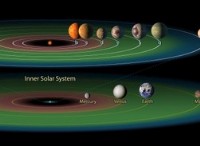
* 케플러의 세 번째 법칙 : 이 법은 행성의 궤도 시대의 광장 (태양 주위의 혁명을 완료하는 데 걸리는 시간)은 태양과의 평균 거리의 큐브에 비례한다고 말합니다.
* 수학적 관계 : 이 관계는 다음과 같이 표현 될 수 있습니다. t² ∝ r³
* t =궤도 기간
* r =태양과의 평균 거리는
* 설명 : 이것은 행성이 태양에서 멀어 질수록 궤도 반경 (R)이 클수록 더 크다는 것을 의미합니다. 비례를 유지하려면 궤도 기간 (t²)의 제곱도 더 커야합니다. 이로 인해 지구의 혁명이 더 길어집니다.
이렇게 생각하십시오 :
수은처럼 태양과 가까운 행성을 상상해보십시오. 작은 궤도 반경이 작고 궤도에 머무르기 위해 더 빨리 움직여야합니다. 해왕성과 마찬가지로 행성은 훨씬 더 큰 궤도 반경을 가지고 있습니다. 궤도에 머무르면 느리게 움직입니다. 이 느린 속도는 더 긴 혁명으로 이어집니다.
요약 :
* 중력 : 태양의 중력 당김은 거리에 따라 약해집니다. 더 멀리 떨어진 행성은 중력이 덜 경험되어 궤도에 머무르기 위해 느리게 움직여야합니다.
* 궤도 경로 : 궤도 반경이 클수록 행성이 하나의 혁명을 완료하기 위해 행성의 거리가 길어야합니다.
그러므로 태양에서 멀리 떨어진 행성은 태양에 가까운 행성에 비해 태양을 공전하는 데 항상 더 오래 걸립니다.