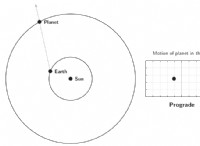
* 케플러의 세 번째 법칙 : 이 법은 행성의 궤도 시대의 광장 (태양 주위의 혁명을 완료하는 데 걸리는 시간)은 태양과의 평균 거리의 큐브에 비례한다고 말합니다.
간단한 용어로 :
* 더 멀리 떨어진 행성은 궤도 기간이 길다. 행성이 태양에서 나오면 태양의 중력이 약해집니다. 이것은 행성이 궤도를 유지하기 위해 더 느린 속도로 더 긴 경로를 이동해야한다는 것을 의미합니다.
* 더 가까운 행성은 궤도 기간이 짧습니다. 태양에 더 가까운 행성은 더 강한 중력 당기기를 경험하여 더 빠른 궤도 속도와 하나의 궤도를 완료하는 데 더 짧은 시간으로 이어집니다.
비유 : 아이가 스윙에 스윙하는 것을 상상해보십시오. 아이가 피벗 포인트에서 멀어 질수록 한 번의 스윙을 완료하는 데 더 오래 걸립니다. 마찬가지로, 태양에서 더 멀리 떨어진 행성은 하나의 궤도를 완료하는 데 시간이 오래 걸립니다.
기타 요인 :
거리는 주요 요인이지만 다른 요인은 궤도 기간에도 영향을 미칩니다.
* 태양의 질량 : 더 거대한 태양은 더 강한 중력을 발휘하여 잠재적으로 궤도 기간에 영향을 미칩니다.
* 행성의 질량 : 태양의 질량은 지배적 인 영향이지만 행성의 질량은 궤도 기간을 결정하는 데 작은 역할을합니다.
결론 : 태양으로부터의 행성의 거리는 궤도 기간이 다른 주된 이유입니다. 행성은 중력이 약하고 더 긴 궤도 경로로 인해 궤도에 더 오래 걸립니다. 이 관계는 Kepler의 제 3 법칙에 의해 설명되며, 거리와 궤도 기간 간의 기본 관계를 설명합니다.