자연의 숨겨진 질서에 대한 조감도

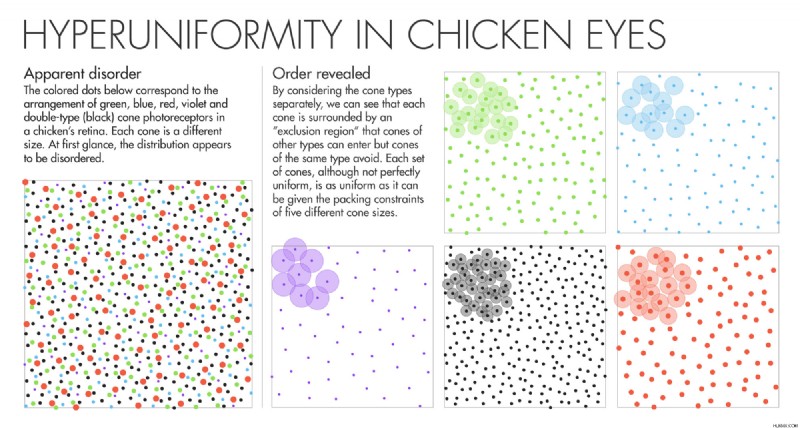
7 년 전, Joe Corbo는 닭의 눈을 쳐다보고 놀라운 것을 보았습니다. 망막을 카펫 (닭에서 분리하고 현미경으로 장착 한)은 5 가지 색상과 크기의 폴카 점으로 나타났습니다. 그러나 Corbo는 인간의 눈에 무작위로 분산 된 원뿔이나 많은 물고기의 눈에 깔끔한 원뿔 줄과는 달리 닭의 원뿔은 우연히 있지만 놀랍도록 균일 한 분포를 가지고 있음을 관찰했습니다. 점의 위치는 눈에 띄는 규칙을 따르지 않았지만 점트는 너무 가까이 나거나 너무 멀리 떨어져 있지 않았습니다. 5 개의 산재 된 원뿔 세트와 함께 함께, 그들 모두는 무작위성과 규칙 성의 동일한 체포 혼합을 나타냈다. 세인트 루이스에있는 워싱턴 대학교에서 생물학 연구소를 운영하는 코보 (Corbo)는 푹 빠졌다.

"이러한 패턴을 보는 것은 매우 아름답습니다."라고 그는 말했습니다. "우리는 아름다움에 의해 포착되었으며, 순전히 호기심에서 패턴을 더 잘 이해하려는 욕구를 가졌습니다." 그와 그의 협력자들은 또한 패턴의 기능과 그들이 어떻게 생성되었는지 알아 내기를 희망했습니다. 그는이 같은 질문이 수많은 다른 맥락에서 묻고 있거나 수학과 물리학을 통해 모든 숨겨진 순서의 첫 번째 생물학적 표현을 발견했다는 것을 알지 못했습니다.

Corbo는 Bird Retinas가 무엇이든 할 일이 아마도해야 할 일이라는 것을 알고있었습니다. Avian Vision은 훌륭하게 잘 작동합니다 (예 :Eagles가 1 마일 높이에서 생쥐를 발견 할 수있게 함), 그의 실험실은이를 만드는 진화 적 적응을 연구합니다. 이 속성들 중 다수는 3 억 년 전에 공룡과 프로토 마말을 일으킨 도마뱀 같은 생물의 새들에게 전달 된 것으로 여겨집니다. 조류의 조상 인 Dinos는 행성에 휴식을 취했지만, 포유류 친족은 어둡고 두려운 야행성이며 점차적으로 색상을 잃어 버렸습니다. 포유류의 원뿔 유형은 두 가지로 떨어졌습니다. 약 3 천만 년 전, 우리의 영장류 조상의 원뿔 중 하나는 기존의 청색 감지 원뿔과 함께 우리에게 삼형 비전을 제공하는 두 개의 빨간색 및 녹색 감지로 나뉘 었습니다. 그러나 우리의 원뿔, 특히 새로운 빨간색과 녹색의 원뿔은 덩어리, 산란 분포와 샘플 라이트를 불안하게합니다.

새 눈은 최적화하는 데 더 오래 걸렸습니다. 그들의 높은 원뿔 수와 함께, 그들은 세포의 훨씬 더 규칙적인 간격을 달성합니다. 그러나 왜 Corbo와 동료들이 궁금해하는 이유는 진화가 그리드의 완벽한 규칙 성이나 "격자"분포를 선택하지 않았는가? 그들이 망막에서 관찰 한 이상하고 분류 할 수없는 패턴은 모든 알 수없는 제약 세트를 최적화하는 것이 었습니다. 이것들이 무엇인지, 패턴이 무엇인지, 그리고 조류 시각 시스템이 어떻게 달성했는지는 불분명했습니다. 생물 학자들은 망막의 규칙 성을 정량화하기 위해 최선을 다했지만, 이것은 낯선 지형이었고 도움이 필요했습니다. 2012 년 Corbo는 Princeton University의 이론 화학 교수 인 Salvatore Torquato와“Packing”으로 알려진 징계 전문가에게 연락했습니다. 포장 문제는 주어진 수의 치수 (망막 2의 경우)에서 물체 (예 :5 가지 크기의 원뿔 셀)를 포장하는 가장 밀도가 가장 높은 방법에 대해 묻습니다. Corbo는“이러한 시스템이 최적으로 포장되어 있는지에 대한이 질문을 원했습니다. 흥미로운 Torquato는 망막 패턴의 디지털 이미지에 대한 알고리즘을 실행했으며“놀랍습니다”라고 Corbo는 다음과 같이 회상했습니다.“이 시스템에서 많은 무기 또는 물리적 시스템에서 볼 수있는 것과 동일한 현상이 발생하는 것을 보려고했습니다.”

Torquato는 2000 년대 초 부터이 숨겨진 질서를 연구 해 왔는데, 그는“과도하게”라고 불렀습니다. (이 용어는 Rutgers University의 Joel Lebowitz와 같은시기에 동시에“초 저명성”에 대해 승리했습니다.) 그 이후로, 그것은 빠르게 확장되는 시스템 제품군에서 나타났습니다. 조류 눈을 넘어서, 과도한 성은 정적 결정이라고 불리는 물질뿐만 아니라 무작위 숫자, 우주의 대규모 구조, 양자 앙상블 및 에멀젼 및 콜로이드와 같은 부드러운 미래 시스템으로 가득 찬 수학적 행렬에서 발견됩니다.

과학자들은 마치 우주와 함께 whack-a-mole을 연주하는 것처럼 새로운 장소에서 나타날 때 거의 항상 놀랍습니다. 그들은 여전히 ​​이러한 사건의 기초가되는 통일 개념을 찾고 있습니다. 그 과정에서 그들은 기술적으로 유용한 것을 증명할 수있는 과민성 재료의 새로운 특성을 발견했습니다.

Microsoft Research New England의 수학자이자 포장 전문가 인 Henry Cohn은 수학적 관점에서“더 우아하고 개념적으로 설득력있는 것 같습니다. "반면에, 그것에 대해 나를 놀라게하는 것은 응용 프로그램의 잠재적 폭입니다."

비밀 질서

Torquato는 올 봄 프린스턴 사무소에서“이론적으로 설명하고 이론적으로 설명하고 단순하면서도 놀라운 예를 밝히고 단순하면서도 놀라운 예를 식별하고 단순하면서도 놀라운 예를 밝혀 냈습니다. "그 시스템은 과잉이 균일합니다."

대리석은 기술적으로 "최대 임의의 잼 포장"이라고 불리는 배열에 속하며 공간의 64 %를 채 웁니다. (나머지는 빈 공기입니다.) 이것은 구체의 가장 밀도가 높은 배열보다 작습니다. 그러나 격자 패킹이 항상 가능하지는 않습니다. 상자의 대리석을 수정 배열로 쉽게 흔들 수는 없습니다. Torquate는 닭 눈의 원뿔과 같은 5 가지 크기의 물체를 배열하여 격자를 형성 할 수 없다고 설명했다.

원뿔의 스탠드 인으로서 탁상에서 동전을 고려하십시오. Torquato는“동전을 복용하고 동전을 압축하려고하면 동전이 삼각 격자로 들어가는 것을 좋아합니다. 그러나 페니와 함께 니켈을 던지고“결정화를 막는 것을 막으십시오. 이제 5 개의 다른 구성 요소가 있다면 (분기에 던지고, 다임을 던지십시오) 결정화를 더욱 억제합니다.” 마찬가지로, 기하학은 조류 원뿔 세포를 무질서해야한다. 그러나 망막이 가능한 한 균일하게 빛을 샘플링하라는 경쟁의 진화 적 요구가 있으며, 푸른 원뿔은 다른 푸른 원뿔에서 멀리 떨어져 있고, 다른 빨간색과는 거리가 멀다는 등. Torquato는 이러한 제약의 균형을 맞추면서“무질서한 과민성을 위해 정착한다”고 말했다.

초고성 성은 새들에게 두 세계의 최고를 제공합니다. 5 개의 원뿔 유형은 거의 불균일 한 모자이크로 배열되어 경이로운 색상 해상도를 제공합니다. 그러나“눈으로 감지 할 수없는 숨겨진 순서”라고 그는 말했다.

시스템이 hyperuniform인지 여부를 결정하려면 링 토스 게임처럼 작동하는 알고리즘이 필요합니다. 먼저, Torquato는 말하면서, 순서대로의 순서의 격자에 반복적으로 반지를 던지는 것을 상상하고, 매번 착륙 할 때마다 링 내부의 점수를 계산합니다. 캡처 된 도트의 수는 하나의 링 던지에서 다음 링 던지기로 변동하지만 그다지 많지는 않습니다. 반지의 내부는 항상 고정 된 도트 블록을 덮기 때문입니다. 캡처 된 도트 수의 유일한 변화는 링 주변을 따라 발생합니다. 링의 크기를 늘리면 더 긴 주변에 따라 변화가 발생합니다. 그리고 격자로 인해 캡처 된 도트 (또는 격자의“밀도 변동”)의 변화는 링 주변의 길이에 비례하여 자랍니다. (공간 치수가 높을수록 밀도 변동은 차원의 수에 비례하여 스케일링됩니다.)

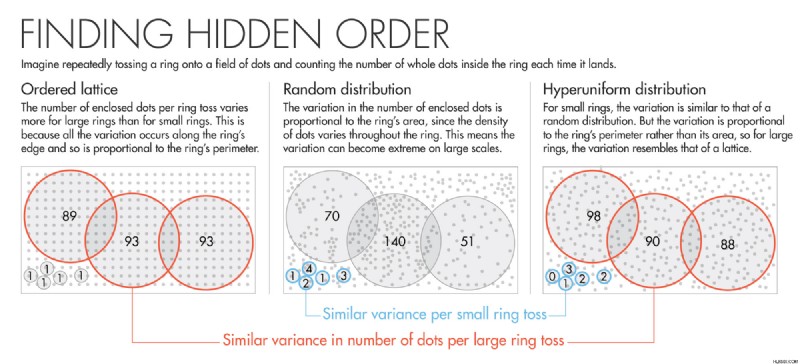
이제 상관되지 않은 도트의 스미터로 링 토를 연주한다고 상상해보십시오. 틈과 클러스터로 표시되는 임의의 분포입니다. 무작위성의 특징은 링을 더 크게 만들면서 주변이 아닌 링 영역에 비례하여 캡처 된 도트 스케일의 변화가 있다는 것입니다. 결과적으로 대규모에서는 무작위 분포에서 링 토스 사이의 밀도 변동이 격자보다 훨씬 더 극단적입니다.

이 게임은 hyperuniform 분포가 포함될 때 흥미로워집니다. 점은 국소 적으로 무질서이므로 작은 링 크기의 경우 캡처 된 도트의 수는 한 번의 던지기에서 격자보다 더 많은 토스로 변동합니다. 그러나 링을 더 크게 만들면서 밀도 ​​변동은 영역이 아닌 링 주변에 비례하여 자라기 시작합니다. 이는 분포의 대규모 밀도가 격자와 마찬가지로 균일하다는 것을 의미합니다.

과민성 시스템 중에서 연구원들은“구조물의 동물학”을 발견했다고 프린스턴 물리학 자 폴 스타인 하르트 (Paul Steinhardt)는 말했다. 이 시스템에서 밀도 변동의 성장은 링 주변의 다른 전력 (1 ~ 2 사이)에 따라 달라지며 다른 계수를 곱합니다.

"무엇을 의미 하는가?" Torquato가 말했다. “우리는 모릅니다. 진화하고 있습니다. 많은 논문이 나오고 있습니다.”

재료 menagerie

초고성 성은 분명히 다양한 시스템이 수렴하는 상태이지만, 보편성에 대한 설명은 진행중인 작업입니다. Cohn은“나는 과민성을 기본적으로 어떤 종류의 더 깊은 최적화 과정의 특징으로 본다”고 말했다. 그러나 이러한 과정은 "다른 문제에 따라 다를 수 있습니다".

hyperuniform 시스템은 두 가지 주요 클래스에 속합니다. 제 1 클래스의 정유류와 같은 사람들 (인터 로크 된 원자가 반복 패턴을 따르지 않지만 테셀레이트 공간을 따르는 기괴한 고체)은 평형에 도달하면 입자가 자신의 협정에 정착하는 안정적인 구성 인 쌍곡선 인 것처럼 보입니다. 이러한 평형 시스템에서, 입자들 사이의 상호 반발은 그들을 분리하고 글로벌 과게성을 야기하는 입자들 사이의 상호 반발이다. 비슷한 수학은 조류 눈의 과도 불균일의 출현, 임의 행렬의 고유 값 분포 및 Riemann Zeta 기능의 0- 소수의 사촌을 설명 할 수 있습니다.

다른 클래스는 잘 이해되지 않습니다. 차가운 원자의 흔들린 대리석, 에멀젼, 콜로이드 및 앙상블을 포함하는 이들 "quilibrium"시스템에서, 입자는 서로 충돌하지만 상호력을 발휘하지는 않는다. 외부 힘은 시스템에 적용되어 과민성 상태로 이동해야합니다. 비평 형 클래스 내에는 더 다루기 쉬운 분열이 있습니다. 지난 가을, 프랑스 리옹에있는 École Normale Supérieure의 Denis Bartolo가 이끄는 물리학 자들은 물리 검토 편지에서보고했다. 이 과민성은 물질의 가역성과 비가역성 사이의 전이를 나타내는 정확한 진폭에서 슬로스 링하여 에멀젼에서 유도 될 수있다 :이 임계 진폭보다 부드럽게 부드럽게 슬로스를 쳤을 때, 입자에 매달린 입자는 각 슬로시 이후 이전의 상대 위치로 돌아갑니다. 더 세게 슬러스되면 입자의 움직임이 반전되지 않습니다. Bartolo의 연구는 가역성의 시작과 그러한 비 quilibrium 시스템에서 과민성의 출현 사이의 근본적인 (완전히 형성되지는 않았지만) 연결을 제안합니다. 한편 최대 임의의 방해가 된 포장은 완전히 다른 이야기입니다. "두 물리학을 연결할 수 있습니까?" 바르톨로가 말했다. "아니요. 별말씀을요. 우리는이 두 가지 매우 다른 물리적 시스템 세트에 왜 과도 성이 나타나는지 전혀 모른다.”