다음은 추방을 일으키는 방법입니다. 많은 자연 주의자들에게 세상을 단순화하도록 요청하십시오. 우리는 보통 동물, 식물, 미생물, 지구, 바람 및 불 사이의 복잡한 상호 작용 웹의 측면에서 다윈이“얽힌 은행”이라고 불렀습니다. 광범위한 일반화로 은행의 복잡성을 줄이는 것은 부정직 한 것처럼 보일 수 있습니다.
따라서 위스콘신 대학교의 이론 생태학자인 토니 아이브스 (Tony Ives)는 2013 년 미국 생태 학회 회의에서 일반 법률을 찾아야하는지에 대한 투표를 요구함으로써 동료들을 자극했을 때, 그 방의 3 분의 2가 투표권을 얻지 못했을 것입니다.
.회의론에도 불구하고 단순화에 의해 가능한 일반적인 법률의 종류는 놀라운 예측 능력을 가지고 있습니다. 그들은 너무 큰 생태계에 너무 큰 샘플을 샘플링하기에는 얼마나 많은 종 또는 서식지 파괴 후 얼마나 많은 종을 잃을 수 있는지 계산할 수 있습니다.
아마도 물리학 훈련 후 생물학을 시작했기 때문에이 일반 법에서 아름다움을 찾는 생태 학자입니다. 물리학에서 마지막으로 걱정하는 것은 가스의 한 분자와 다른 분자의 차이점입니다. 개인적으로 좋아하는 전자는 아무도 없습니다. 압력, 부피 및 온도와 관련된 이상적인 가스 법칙은 산소와 질소에서도 똑같이 잘 유지됩니다. 액체와 가스 사이의 위상 전이는 특정 금속의 자화와 같은 방식으로 행동합니다.
왜 생태계가 이상적인 가스만큼 아름답게 완벽하지 않아야하며, 왜 생태 학자들이 물리학 자만에 힘을 예측할 수 없습니까? 이 질문들에 대한 답은 단지“그렇다”와“할 수있다”는 것일 수 있습니다. 그러나 특정 관점에서 볼 때만
1980 년대에 뉴 멕시코 대학교 (University of New Mexico)의 짐 브라운 (Jim Brown)과 브리검 영 대학교 (Brigham Youngivers)의 브라이언 메리어 (Brian Maurer)는 거시 생태학이라는 용어를 만들어 자연의 출현 패턴을 찾는 연구원들에게 이름과 지적 집을 지어 주었다. 소규모의 많은 생태 학적 연구에 좌절 한 거시 기술 학자들은 시간과 공간에서 자연을 광범위하게 묘사 할 수있는 패턴과 이론을 찾고있었습니다.
Brown과 Maurer는 많은 생태 학적 현상에서 규칙성에 크게 영향을 받았습니다. 종-지역 곡선이라고 불리는이 중 하나는 19 세기에 다시 발견되었고 1921 년에 공식화되었습니다. 그 곡선은 자연 주의자들이 뒷마당, 사바나, 숲에 자리 잡은 음모에서 발견 된 종의 수 (식물, 곤충, 포유류 등)의 수를 세었을 때 나타났습니다. 그들은 예상대로 음모의 면적에 따라 종의 수가 증가한다는 것을 발견했습니다. 그러나 음모 크기가 계속 증가함에 따라 종의 수 증가율이 고원으로 시작되었습니다. 더욱 주목할만한, 동일한 기본 종-지역 곡선이 종이나 서식지에 관계없이 발견되었습니다. 수학적으로 말하면, 곡선은 전력법을 따랐으며, 이로 인해 종 수의 변화는 해당 지역의 제곱근의 제곱근에 비례하여 증가했습니다.
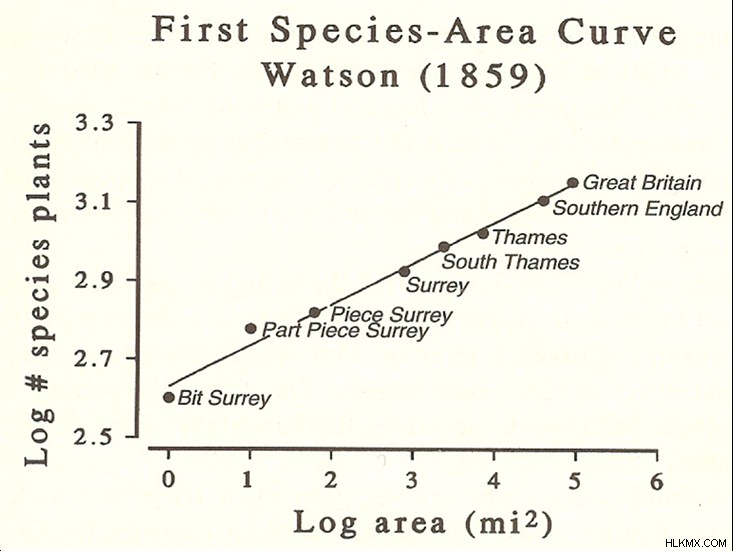
권력 법은 과학에서 일반적이며 물리학에서 보편성의 정의 특징입니다. 그들은 온도가 증가함에 따라 자석의 강도, 지진 빈도 대 크기 및 도시 생산성을 모집단의 함수로 묘사합니다. 많은 생태 학자들에게 종-지역 곡선은 신경을칩니다. 그것은 충분히 큰 규모로 생태계의 구체적인 세부 사항, 즉 생태 학자의 마음에 가까이 있고 사랑하는“얽힌 은행”은 상당히 중요하지 않다고 제안합니다. 특유의 씻겨지고 생태 시스템은 다른 과학에서 넓은 이질적인 시스템의 넓은 습격과 놀랍게도 비슷해 보이기 시작합니다.
종-영역 곡선의 보편성은 생태 학자들이 그것을 이해하기 위해 구축 한 모델에서 풍부하게 분명해졌습니다. 2001 년, Princeton University, Steve Hubbell의 생태 학자는 먹이 사슬의 동일한 부분에있는 개인 간의 선택적 차이 (진화 적 이점 또는 불리한 차이)가 관련이 없다는 급진적 인 가정을 바탕으로 모델을 개발했습니다. 그것은 개별 결과가 일종의 생태 학적 룰렛이라는 것을 의미합니다. 일부 종은 운이 좋으며, 공간에 걸쳐 넓고 풍부한 분포로 끝나는 반면, 다른 종은 비교적 드물게됩니다. 분석 방정식과 컴퓨터 시뮬레이션의 조합을 통해 통합 중립 생물 다양성 이론이라고 불리는 그의 모델은 놀랍게도 현실적으로 보이는 종-영역 곡선을 예측했습니다. 그 성공은 식물, 동물 및 유기체가 거의 동일한 통계적 자리 표시 자들로 대체 된이 잔인하게 단순화 된 실제 생태계 버전에 기반을 두었습니다.
물리 훈련의 또 다른 생태 학자 인 John Harte는 종-영역 곡선이 중립 이론보다 훨씬 덜 생태적 메커니즘으로 이해 될 수 있는지 궁금해했다. Harte는 열역학 및 정보 이론에서 취한 아이디어를 바탕으로 생태학의 최대 엔트로피 이론을 개발했습니다. 엔트로피는 시스템의 장애의 척도이며, 열역학에 사용되어 고정 된 부피로 동일한 가스 분자의 가장 가능성이 높은 배열을 계산합니다. 더 많은 장애가 일반적으로 승리합니다. Harte는 특정 제약 하에서 종의 공간 분포를 가지고 놀면서 최대 엔트로피 이론을 사용하여 인도의 서부 가츠 산맥 전체에 걸쳐 나무 종의 수를 예측했습니다. 생태 편지에 출판 된 그들의 추정치 , 약 900 가지 종류의 계산 된 나무 중 10 %에 빠졌습니다. Harte는 개별 나무의 세부 사항과 그 재생산 또는 종자 분산을 고려하지 않았습니다. 자신의 작업은 순전히 정보 이론 영역의 원칙에 의해 주도되었습니다.
.종들이 어떻게 경쟁하고 서로 다른지에 대한 세부 사항을 무시함으로써, 최대 엔트로피와 중립 이론은 생태계의 지저분하고 복잡한 엉킴을 이상적인 가스의 이상적인 완전성으로 변형시킵니다. 그렇게함으로써 그들은 생태 학자들이 물리와 같은 능력을 예측하고 설명 할 수있게 해주었다. 그러나 두 모델 모두 논란의 여지가 있습니다. 이러한 세부 사항은 생태 학자들이 평생 조사하는 데 보낼 수있는 것과 정확히 무엇이 중요하지 않다는 것을 암시하는 두 가지 이론이 있습니다.
.이러한 공간 예측이 정확하지만 잘못된 이유가 있다면 어떨까요? 일반 생태 모델에는 실제 생태 학적 세부 사항과 메커니즘이 포함되어야 할 수도 있지만 이러한 세부 사항을 무시하지만 여전히 성공하는 모델은 종-영역 곡선과 같은 공간 패턴으로 제한되는 플루크입니다. 찾는 한 가지 방법은 이러한 모델을 다른 차원으로 확장하는 것이 었습니다. 나는 시간을 선택했다.
생태 학자는 50 년 안에 얼마나 많은 나무 종이 죽을 지 추정하기 위해 무엇을 할 것인가? 수천 년 전에 몇 개의 계보는 어떻습니까? 종-지역 곡선을 모델링하는 것과 유사한 이론은 공간 대신 시간에 초점을 맞춘 편리합니다. 그래서 나는 이전에 나와 협력했던 동료 인 Tom Sharpton과 Steve Kembel을 모집하여 하나를 건설했습니다.
.박테리아는 명백한 주제처럼 보였습니다. 부분적으로는 엄청나게 풍부하기 때문에 부분적으로 DNA 서열 데이터가 우리에게 진화 역사에 대한 창을 제공하기 때문입니다. 우리의 계획은 종-지역 곡선에서와 마찬가지로 종의 수를 세는 것이 었습니다. 그러나 지역 대신에 우리는 어느 정도의 시간을 사용합니다.
우리는 박테리아 사이의 DNA 서열을 비교하고 생명의 나무를 끌어 들여 그 측정을 구성했습니다. 나무의 각 가지는 새로운 박테리아 계보를 나타 냈습니다. 나무의 종들 사이의 평균 진화 거리 (또는 분기 길이)는 시간이 지남에 따라 관련성을 정량화했습니다. 우리가 샘플링 한 미생물은 인간의 비강, 인간 대변, 식물 잎 표면, 남극 바다 및 영국 수로의 물을 포함하여 약 25 개의 다른 서식지에서 나왔습니다.
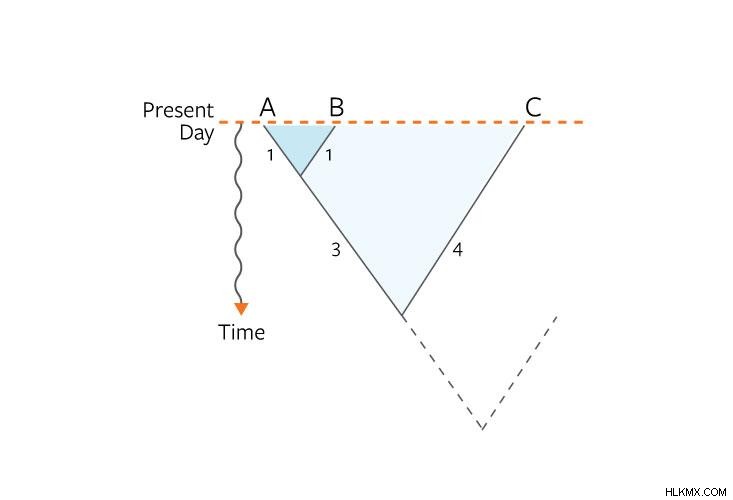
우리가 종 수에 대한 평균 진화 거리를 음모했을 때, 우리는 또 다른 차원의 생태학에 전력법이 숨어있는 것을 발견했습니다. 처음에는 거리가 빠르게 증가한 다음 종-영역 곡선과 같은 방식으로 느려지기 시작했습니다. 이 행동의 이유는 현재 명확하지 않습니다. 한 가지 가능성은 공간적 및 시간적 스케일링 행동이 "파라스티스"에 의해 영향을 받는다. 여기서 정체 기간은 빠른 다양 화 기간에 의해 구두점이있다. 우리의 박테리아 나무에서 우리는 이러한 버스트 팽창이 전력법에 의해 설명 된 프랙탈 분포를 가지고 있으며 시간과 공간을 통해 종의 방사선을 가리킬 수 있음을 발견했습니다.
.우리가 진화의 거리와 다각화에 대한 전력 법칙은 다시 한 번 가장 큰 규모에서 단순하고 기계적이며 비교적 세부적인 생태 관점으로 다시 한 번. 그들은 공간 패턴에 대해 제안 된 것만 큼 단순하지 않습니다. 그들은 거시 생태 학적 패턴을 설명하기 위해 실제 생태 학적, 진화 적 메커니즘이 필요한 스펙트럼을 적어도 한 걸음 뒤로 내려갑니다.
또 다른 생태 학자는 한 번 나에게 물었다. 우리는 스케일링에서 무엇을 배운 적이 있습니까? 공정한 질문입니다. 종-지역 곡선을 사용한 적이없는 많은 생태 학자들이 있습니다. 저에게는 지적 스릴과 도전이 있으며, 다른 시스템에서 예상치 못한 유사성을 발견 할 때 놀라움의 요소가 있습니다. 스케일링이 가능하게하는 예측의 힘도 있습니다. 우리가 거시 생태학을 이해하는 데 실제로 도움이되는 이론을 개발할 수 있다면, 오늘날의 아마존 다양성 상실이 100 년 안에 열대를 어떻게 변화 시킬지 더 잘 추정 할 수 있습니다. 또는 인간 장에서 박테리아의 상호 작용이 미래를 바꿀 수있는 방법.
더 많은 것이 있습니다. 생태에서는 곤충에서 새, 잔디, 레드 우드에 이르기까지 항상 큰 이질성이있을 것입니다. 우리는 집계 된 패턴에 관한 것이 아니라 다른 유기체와 종의 차이를 신경 쓰고 신경을 쓸 수 있습니다. 우리는 생태학의 보편적이고 간단한 스케일링 패턴에 대해 배우면서 새로운 도전에 직면 해 있습니다. 자연사와 다른 유기체와 시스템 간의 훌륭한 세부 사항과 함께 집계 된 패턴의 스케일링에서 배우는 일반성을 어떻게 통합합니까?
생태 학회 회의에서 IVES의 질문에 유용한 보완이 있습니다. 생태학이 일반적인 법을 추구 해야하는지 여부가 아니라, 법을 쫓는 사람들과 그 법을 창조하는 엉킴에 집중하는 사람들이 함께 일할 수있는 방법입니다. 우리가 그 연결을 알아낼 때 배울 것이 많을 것입니다.
James O'Dwyer는 Urbana-Champaign에있는 일리노이 대학의 식물 생물학과의 이론 생태학 자입니다.
참조
1. Fox, J. Esa Monday 검토 :Tony Ives Rocks. 동적 생태학 Dynamicecology.wordpress.com (2013).
2. Harte, J., Smith, A.B., &Storch, D. 생물 다양성 척도는 보편적 인 종-영역 곡선을 가진 플롯에서 생물체까지. 생태 편지 12 , 789-797 (2009).
3. O'Dwyer, J.P., Kembel, S.W. 및 Sharpton, T.J. 미생물에 대한 진화 역사 테스트 생물 다양성 이론의 백본. 국립 과학 아카데미의 절차 112 , 8356-8361 (2015).
edhv, www.edhv.nl (네덜란드 아인트호벤)