2016 년 온화한 가을에 헝가리 수학자 Gábor Domokos는 필라델피아에서 지구 물리학 자 Douglas Jerolmack의 문앞에 도착했습니다. 도모 코스는 그에게 그의 여행 가방, 나쁜 추위, 불타는 비밀을 가지고 다녔습니다.
두 남자는 집 뒤의 자갈을 가로 질러 걸어 가서 Jerolmack의 아내가 타코 카트를 달렸습니다. 그들의 발은 분쇄 된 석회암 위로 뭉개졌습니다. Domokos가 지적했습니다.
"이 자갈 조각들은 각각 얼마나 많은면이 있습니까?" 그는 말했다. 그런 다음 그는 웃었다. "내가 숫자가 항상 여섯여 명의 어딘가에 있다고 말하면 어떻게 될까요?" 그런 다음 그는 더 큰 질문을했습니다. 세상이 큐브로 만들어지면?
처음에 Jerolmack은 반대했습니다. 집은 벽돌로 지어 질 수 있지만 지구는 바위로 만들어졌습니다. 분명히 바위는 다양합니다. 운모 조각으로 시트로; 크게 정의 된 축에 결정이 균열됩니다. 그러나 Domokos는 수학만으로도 무작위로 부러진 암석은 평균적으로 6 개의 얼굴과 8 개의 정점이있는 모양으로 갈라질 것이라고 주장했다. 함께 고려하여, 그들은 모두 이상적인 큐브에 수렴하는 그림자 같은 근사치 일 것입니다. 도모 코스는 수학적으로 입증했다고 그는 말했다. 이제 그는 이것이 자연이하는 일임을 보여주기 위해 Jerolmack의 도움이 필요했습니다.
펜실베이니아 대학교 (University of Pennsylvania)의 교수 인 제롤마 맥 (Jerolmack)은“자연 세계에서는 정확한 예측을 가진 기하학적이었다. “도대체 어떻게 자연이 이런 일이 일어나게됩니까?”
향후 몇 년 동안, 쌍은 미세한 조각에서 암석 노두, 행성 표면, 플라톤의 timaeus 까지 기하학적 시력을 쫓았습니다. , 추가적인 신비주의 공기로 프로젝트를 질식시킵니다. 기원전 360 년경에 글을 쓰는 기초 그리스 철학자는 5 개의 플라톤 고체를 지구, 공기, 불, 물 및 별 물건의 5 가지 요소와 일치시켰다. 예측이나 행운 또는 둘 다, 플라톤 쌍 큐브, 지구와 함께 가장 쌓일 수있는 모양입니다. Jerolmack은“오, 오, 이제 우리는 조금은 형이상학을 얻고 있습니다.


그러나 그들은 본질적으로 cuboid 평균과 같은 이론으로 설명 할 수있는 몇 가지 비 큐브를 계속 찾았습니다. 그들은 새로운 수학적 프레임 워크로 끝났습니다. 그들의 논문이 올해 초에 출판되었을 때, 그것은 특히 난해한 해리포터 소설과 같은 제목이었다 :“플라톤의 큐브와 파편화의 자연 지오메트리.”
.Quanta 에 의해 접촉 한 몇몇 지구 물리학 자 동일한 수학적 프레임 워크가 금이 간 절벽면에서 침식을 이해하거나 위험한 암석 슬라이드를 방지하는 것과 같은 문제에 도움이 될 수 있다고 가정합니다. 에든버러 대학교 지오메트리 학자 미카엘 아탈 (Mikaël Attal)은“정말 흥미 롭습니다. 다른 리뷰어 인 Vanderbilt 지구 물리학 자 David Furbish는 다음과 같이 말했습니다.
가능한 모든 휴식
그가 필라델피아에 오기 훨씬 전에 Domokos는 더 무해한 수학적 질문을했습니다.
당신이 무언가를 많은 조각으로 골절한다고 가정 해 봅시다. 당신은 이제 모자이크를 가지고 있습니다 :고대 로마 목욕의 바닥과 같이 겹치거나 틈없이 타일 수있는 모양의 모음. 더욱이 그 모양이 모두 볼록하고 들여 쓰기가 없다고 가정합니다.
첫 번째 Domokos는 형상만으로도 평균적으로 어떤 모양이 그런 종류의 모자이크를 구성 할 수 있는지 예측할 수 있는지 확인하고 싶었습니다. 그런 다음 그는 당신이 찾을 수있는 다른 모든 모양의 컬렉션을 설명 할 수 있기를 원했습니다.
두 가지 차원으로 아무것도 부수지 않고 시도해 볼 수 있습니다. 종이 한 장을 가져 가십시오. 페이지를 두 조각으로 나누는 임의의 슬라이스를 만드십시오. 그런 다음 두 다각형 각각을 통해 다른 임의의 슬라이스를 만듭니다. 이 랜덤 프로세스를 몇 번 더 반복하십시오. 그런 다음 모든 종이의 모든 비트에 대한 정점 수를 계산하고 평균화합니다.
기하학 학생의 경우 답변을 예측하는 것이 어렵지 않습니다. Domokos는“저는 2 시간 이내에 그 공식을 도출 할 수있는 맥주 상자를 내기합니다. 조각은 평균 4 개의 정점과 4면으로 사각형으로 평균해야합니다.
3 차원에서 동일한 문제를 고려할 수도 있습니다. 약 50 년 전, 러시아 핵 물리학 자, 반체제 및 노벨 평화상 수상자 인 Andrei Dmitrievich Sakharov는 아내와 양배추의 머리를 자르면서 같은 문제를 제기했습니다. 양배추 조각에는 평균적으로 몇 개의 정점이 있어야합니까? Sakharov는 전설적인 소비에트 수학자 블라디미르 Igorevich Arnold와 학생에게 문제를 전달했습니다. 그러나 그것을 해결하려는 그들의 노력은 불완전했고 크게 잊혀졌습니다.

이 작품을 알지 못한 Domokos는 큐브를 대답으로 지적한 증거를 썼습니다. 그러나 그는 두 번 확인하고 싶었고, 같은 문제에 대한 답이 이미 존재한다면, 독일 수학자 Wolfgang Weil과 Geometry 분야의 80 세의 타이탄 인 Rolf Schneider에 의해 불가분의 양에 잠겨있을 것이라고 의심했다. Domokos는 전문 수학자이지만 텍스트도 어려운 것을 발견했습니다.
Domokos는“저를 위해 그 책의 그 부분을 기꺼이 읽고 기꺼이 그것을 인간의 언어로 번역하려는 사람을 찾았습니다. 그는 여러 차원에 대한 정리를 발견했습니다. 그것은 큐브가 실제로 3D 답변임을 확인했습니다.
이제 Domokos는 평평한 표면 또는 3 차원 블록을 분할하여 생성 된 평균 모양을 가졌습니다. 그러나 더 큰 퀘스트가 나타났습니다. Domokos는 그가 평균뿐만 아니라 잠재력에 대한 수학적 설명을 개발할 수 있음을 깨달았습니다. 무언가가 무너질 때 어떤 모양의 컬렉션이 수학적으로 가능합니까?
무언가가 무너진 후 생성 된 모양은 모자이크입니다. 그들은 겹치거나 틈없이 함께 맞습니다. 예를 들어, 이러한 컷업 사각형은 쉽게 함께 타일을 타일하여 모자이크를 2 차원으로 채울 수 있습니다. 따라서 수학자들이 보로 노이 패턴이라고 부르는 이상적인 사례에서 헥사 곤은 할 수 있습니다. 하지만 펜타곤? 옥타곤? 그들은 타일이 아닙니다.
Mosaics를 올바르게 분류하기 위해 Domokos는 두 숫자로 설명하기 시작했습니다. 첫 번째는 셀당 평균 정점 수입니다. 두 번째는 각 정점을 공유하는 다른 세포의 평균 수입니다. 예를 들어, 각각의 세포는 육각형 목욕 타일의 모자이크에서 6 개의 정점이있는 육각형이다. 그리고 각 정점은 3 개의 16 진수로 공유됩니다.
모자이크에서는이 두 매개 변수의 특정 조합 만 작동하여 좁은 모양의 모양을 형성하여 무언가가 떨어질 수 있습니다.
다시 한 번,이 전체 스와 스는 2 차원에서 찾기가 쉽지만 3 개는 훨씬 더 어렵습니다. 물론 큐브는 3D로 잘 쌓여 있지만 3D 버전의 Voronoi 패턴을 형성하는 모양을 포함하여 다른 모양 조합도 마찬가지입니다. 문제를 실현 가능하게하기 위해 Domokos는 동일한 정점을 공유하는 질서있는 볼록한 셀로 모자이크로 제한했습니다. 결국 그와 수학자 Zsolt Lángi는 가능한 모든 3 차원 모자이크의 곡선을 스케치 한 새로운 추측을 고안했습니다. 그들은 실험 수학 에 그것을 출판했습니다 그리고“그러면 나는 물론 신인 Rolf Schneider에게 모든 것을 보냈습니다.”Domokos는 말했습니다.
Domokos는“나는 그가이 추측을 어떻게 얻었는지 설명 할 것인지를 물었다. 그러나 그는 그가 알고 있다는 것을 안심시켰다”고 Domokos는 웃으며 말했다. "그것은 모든 일지에서 받아 들여지는 것보다 백 배 더 많은 것을 의미했습니다."
더 중요한 것은 Domokos가 이제 프레임 워크를 가졌다는 것입니다. 수학은 표면과 블록이 침입 할 수있는 모든 패턴을 분류하는 방법을 제공했습니다. 지오메트리는 평평한 표면을 무작위로 조각화하면 거친 사각형으로 나뉘어지고 3 차원에서 동일하게 한 경우 거친 큐브를 생성 할 것이라고 예측했습니다.
.그러나이 중 어느 것도 수학자 소수의 수학자 이외의 다른 사람에게 문제가되는데, 도모 코스
지오메트리에서 지질학으로
Domokos가 2016 년 필라델피아를 통해 흔들렸을 때, 그는 이미 실제 문제에 대해 약간의 진전을 이루었습니다. 부다페스트 기술 및 경제 대학교의 동료들은 부다페스트의 Hármashatárhegy Mountain의 절벽에서 침식 된 백운석 파편을 모았습니다. 며칠에 걸쳐, 큐브에 대한 보편적 음모에 대한 전제가없는 실험실 기술은 수백 개의 곡물에 얼굴과 정점을 힘들게 계산했습니다. 평균적으로? 6 개의 얼굴, 8 개의 정점. 컴퓨터 시뮬레이션 전문가 인 János Török 및 Fragrmentation Physics의 전문가 인 Ferenc Kun과 함께 Domokos는 Cuboid 평균이 석고 및 석회암과 같은 암석 유형에도 나타났습니다.
수학과 초기의 물리적 증거로 Domokos는 그의 아이디어를 기절 한 Jerolmack에게 투구했습니다. Jerolmack은“어떻게 든 그는 주문을했고 다른 모든 것이 잠시 사라집니다.
그들의 동맹은 친숙한 사람이었습니다. 몇 년 전, Domokos는 Gömböc의 존재를 증명함으로써 명성을 얻었습니다. 자연계에 Gömböcs가 존재하는지 확인하기 위해 그는 Jerolmack을 모집했으며, 그는 지구와 화성의 자갈의 반올림을 설명하기 위해 개념을 적용하는 데 도움을주었습니다. 이제 Domokos는 고상한 수학적 개념을 문자 그대로의 돌로 번역하는 데 도움을 요청했습니다.
두 사람은 새로운 계획에 정착했습니다. 플라톤의 큐브가 실제로 자연에 나타나는 것을 증명하기 위해서는 기하학과 소수의 바위 사이의 우연의 반향 이상을 보여줄 필요가있었습니다. 그들은 모든 암석을 고려한 다음 지저분한 지구 물리학을 통해 그리고 지저분한 현실을 통해 어떻게 추상적 인 수학을 퍼질 수 있는지에 대한 설득력있는 이론을 스케치해야했습니다.
Jerolmack은 처음에“모든 것이 효과가있는 것 같았습니다. Domokos의 수학은 암석 파편이 큐브로 평균해야한다고 예측했습니다. 점점 더 많은 실제 암석 파편이 준수하는 것이 기뻤습니다. 그러나 Jerolmack은 곧 이론을 증명하는 것이 규칙 위반 사례에 직면해야한다는 것을 곧 깨달았습니다.
결국, 동일한 기하학은 2 차원과 3 차원 모두에서 존재할 수있는 다른 많은 모자이크 패턴을 설명하기 위해 어휘를 제공했습니다. 그의 머리 꼭대기에서 Jerolmack은 사각형이나 큐브처럼 보이지는 않지만 여전히이 더 큰 공간으로 분류 될 수있는 실제 골절 된 바위를 상상할 수 있습니다.
.아마도 이러한 예는 큐브 세계 이론을 완전히 가라 앉힐 것입니다. 더 유망하게, 아마도 그들은 뚜렷한 상황에서만 발생하고 지질 학자들에게 별도의 교훈을 가지고있을 것입니다. Jerolmack은“나는 그것이 어디에서나 작동하지 않는다는 것을 알고 있었고 그 이유를 알아야한다고 말했다.
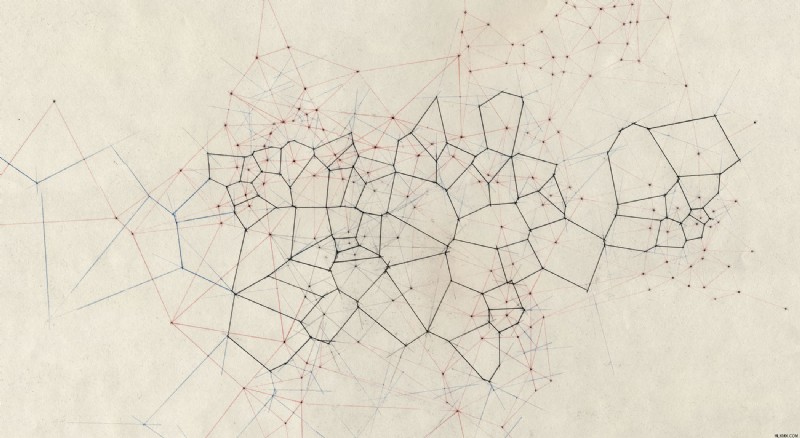
향후 몇 년 동안, 대서양의 양쪽에서 일하면서 Jerolmack과 나머지 팀은 부러진 암석의 실제 사례가 Domokos의 틀 안에있는 곳을 계획하기 시작했습니다. 팀이 본질적으로 2 차원 인 표면 시스템 (알래스카의 영구 동토층, 백운석 노두, 화강암 블록의 노출 된 균열)을 조사했을 때 얇게 썬 종이 시트와 마찬가지로 다각형이 4면과 4 개의 정점을 발견했습니다. 이러한 각 지질 학적 사례는 암석이 단순히 골절 된 곳에서 나타나는 것처럼 보였다. 여기서 Domokos의 예측이 유지되었습니다.
한편, 또 다른 유형의 골절 된 슬래브는 Jerolmack이 원하는 것으로 판명되었습니다. 자체 독특한 이야기를 제외하고는 예외입니다. 건조하고, 갈라지고, 젖고, 치유하고, 다시 갈라지는 진흙 평지는 대략 육각형 보로 노이 패턴에 따라 평균 6면과 6 개의 정점을 가진 세포를 갖습니다. 표면에서 아래쪽으로 굳어지는 냉각 용암으로 만든 암석은 비슷한 모양을 취할 수 있습니다.
말하자면, 이러한 시스템은 다른 유형의 스트레스 하에서 형성되는 경향이있었습니다. 힘이 바위를 밀어내는 대신 바깥쪽으로 끌어 당겼을 때 지오메트리는 지질학을 드러 냈습니다. 그리고 Jerolmack과 Domokos는이 Voronoi 패턴이 상대적으로 드물지만 이전에 고려했던 것보다 훨씬 더 큰 척도에서도 발생할 수 있다고 생각했습니다.
.
크러스트 계수
프로젝트 중간에 팀은 부다페스트에서 만나 3 일 동안 더 많은 자연스러운 사례를 통합하기 위해 회오리 바람을 보냈습니다. 곧 Jerolmack은 그의 컴퓨터에서 새로운 패턴을 뽑았습니다. 지구의 지각 판이 어떻게 맞는 지에 대한 모자이크. 판은 지구 표면의 거의 2 차원 피부 인 석판에 국한됩니다. 패턴은 친숙해 보였고 Jerolmack은 다른 사람들을 불렀습니다. "우리는 와우와 같았다"고 말했다.
눈으로, 판은 마치 마치 직사각형이 아닌 Voronoi 패턴에 닿는 것처럼 보였다. 그런 다음 팀이 계산했습니다. 평평한 평면에서 hexagons의 완벽한 보로 노이 모자이크에서 각 세포에는 6 개의 정점이 있습니다. 실제 지각 판은 평균 5.77 개의 정점입니다.
지구 물리학 자에게는 축하하기에 충분히 가까웠습니다. 수학자에게는 그리 많지 않습니다. “Doug는 기분이 좋았습니다. 그는 지옥처럼 일하고 있었다”고 Domokos는 말했다. "나는 그 차이에 대해 생각하고 있었기 때문에 다음날 우울한 분위기에 빠졌습니다."
Domokos는 밤 동안 집에 갔다. 그는 다시 숫자를 기록했다. 그리고 그것은 그를 때렸다. 육각형의 모자이크는 비행기를 타일 할 수 있습니다. 그러나 지구는 평평한 비행기가 아니며 적어도 YouTube의 특정 구석 외부에 있습니다. 육각형과 펜타곤으로 덮인 축구 공을 생각해보십시오. Domokos는 구 표면의 숫자를 위기에 처해 지구에서 Voronoi Mosaic 세포가 평균 5.77 개의 정점이어야 함을 발견했습니다.
이 통찰력은 연구자들이 지구 물리학에서 주요 공개 질문에 대답하는 데 도움이 될 수 있습니다. 지구의 지각 판은 어떻게 형성 되었습니까? 한 가지 아이디어는 판이 맨틀의 깊은 곳에서 버블 링 대류 세포의 부산물 일뿐입니다. 그러나 반대 캠프는 지구의 빵 껍질이 별도의 시스템이며, 확장되고, 부서지기 쉬웠으며, 깨어났다. Jerolmack은 훨씬 작은 진흙 평지를 연상시키는 관찰 된 보로 노이 판의 패턴이 두 번째 논쟁을지지 할 수 있다고 말했다. Attal은“이것이 종이가 얼마나 중요한지 깨달았습니다. "정말 경이 롭습니다."
공개 휴식
한편 3 차원에서는 입방체 규칙에 대한 예외가 충분히 드물었다. 그리고 그것들도 비정상적인 외향적 인 힘을 시뮬레이션하여 생산 될 수 있습니다. 뚜렷하게 비 큐 비빅 암석 형성 중 하나는 북 아일랜드 해안에 있으며, 파도는 수만 개의 현무암 기둥에 랩이 랩됩니다. 아일랜드에서 이것은 초자연적 존재의 종족의 의붓 폰 인 Clochán na bhfomhórach입니다. 영어 이름은 거인의 둑길입니다.
결정적으로, 이러한 기둥 및 기타 유사한 화산암은 6면입니다. 그러나 Török의 시뮬레이션은 Giant 's Causeway와 같은 모자이크를 2 차원 Voronoi베이스에서 단순히 자란 3 차원 구조로 만들었습니다.
이 팀은 확대 해제에 따르면 플라톤 사각형, 2D 보로 노이 패턴, 그리고 압도적으로 3 차원의 플라톤 큐브를 사용하여 가장 실제 파쇄 된 록 모자이크를 분류 할 수 있다고 팀은 주장했다. 이러한 각 패턴은 지질 학적 이야기를 할 수 있습니다. 그리고 네, 적절한 경고로 세상은 큐브로 만들어 졌다고 말할 수 있습니다.
샬럿 노스 캐롤라이나 대학교 (University of North Carolina)의 지구 과학자 인 Martha-Cary Eppes는“그들은 현실에 대한 모델링 형태를 심사하는 데 실사를했다. “나의 초기 회의론은 모두 끝났다.”
Furbish는“수학은 우리가 암석을 골절하기 시작하면 무작위로 또는 결정적으로할지 여부에 관계없이 특정 가능성 만 있다고 말합니다. “얼마나 영리한가?”
구체적으로, 당신은 아마도 당신은 실제 골절 된 필드 사이트를 가져 가서 정점과 얼굴과 같은 것을 세고, 책임있는 지질 학적 상황에 대해 유추 할 수있을 것입니다.
.펜실베이니아 주립 대학의 기질 학자 인 로마 디비아 세 (Roman Dibiase)는“우리는 이런 식으로 생각할 수있는 데이터가있는 곳이 있습니다. "거인의 둑길보다 미묘한 것을 분별하고 망치로 바위를 때리고 파편이 어떻게 생겼는지 보는 것이 정말 멋진 결과 일 것입니다."
.Jerolmack에 관해서는, 플라톤과의 우연의 관계에 대해 불편한 느낌을받은 후, 그는 그것을 받아 들였습니다. 결국, 그리스 철학자는 이상적인 기하학적 형태가 우주를 이해하는 데 중심이지만 항상 눈에 띄지 않으며 왜곡 된 그림자로만 볼 수 있다고 제안했습니다.
“이것은 말 그대로 우리가 생각할 수있는 가장 직접적인 예입니다. 이러한 모든 관찰의 통계 평균은 큐브입니다.”라고 Jerolmack은 말했습니다.
"하지만 큐브는 결코 존재하지 않습니다."
이 기사는 에 재 인쇄되었습니다 wired.com .