수치 계산은 많은 과학 분야에서 매우 중요한 것으로 널리 알려져 있습니다. 비선형 과학 및 복잡한 시스템에 대한 많은 결론은 디지털 컴퓨터의 시뮬레이션에 따라 그려졌습니다. 이 중요성은 널리 인식되지만 컴퓨터 작동 방식은 일반적으로 자세히 알려지지 않았습니다.
다음 예제로 토론을 시작합시다. 물류 맵으로 알려진 다음 방정식이 되십시오 :
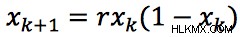
이 방정식의 아이디어는 매우 간단합니다. 우리는 단계 k =0에서 시뮬레이션을 시작합니다.이 단계에서는 초기 조건이 있습니다. r =4를 가정하고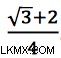 
다음 단계에서는 ¼을 얻는 것을 쉽게 계산하기가 쉽습니다. 세 번째 반복 후 정답이 멈출 것입니다 - 고정 - ¾의 값으로.
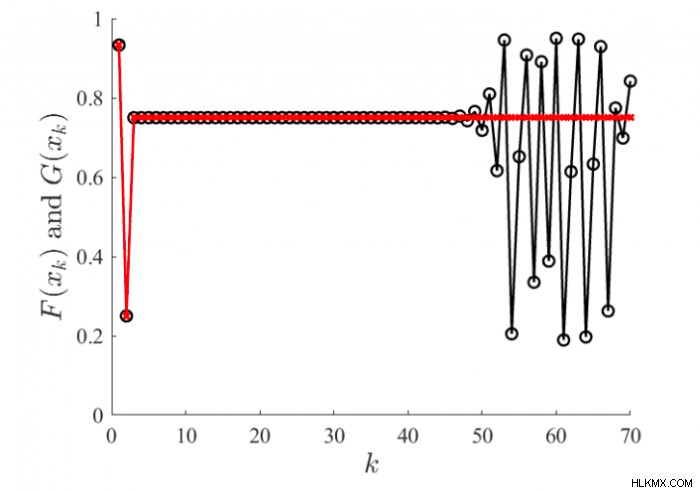
상용 소프트웨어를 사용 하여이 계산을 진행하며 그림 1의 결과를 얻을 수 있습니다. 빨간색 선과 검은 색 라인은 방정식 f 에 의해 생성됩니다. ( x k ) =4 x k (1 - x k ), g ( x k ) =4 x k - 4 x k . 방정식은 수학적으로 동등하지만 컴퓨터는 F에 대한 안정되고 고정 된 결과를 생성하고 G. 비선형 동적 이론과 미적분학 및 미분 방정식에 기반한 수학 분야는 이것을 제대로 설명 할 수 없습니다.
.
최근의 연구에서“부분적인 접근법을 사용한 간격 컴퓨팅주기 궤도”라는 제목의 연구에서, 우리는이 상황을 인식하고 최소한이 상황을 줄이기위한 접근법을 개발했습니다. 기본 아이디어는 부동 소수점을 기반으로 한 대부분의 수치 계산이 좋은 결과를 보장하기 위해 구축되거나 기술적 인 용어로 사용 된 비트 수에 따라 정밀한 결과를 보장하기 위해 구축된다는 사실에 의존합니다.
그림 1의 예는이 예제를 매우 어려운 기능으로 바꾸는 두 가지 기능을 나타냅니다. 첫째, 계산은 기본 산술 연산 세트입니다. 두 번째로 가장 중요한 것은 처음에 매우 작은 오류가 기하 급수적으로 증가하는 재발이 있습니다. 이 논문에서는 기능의 일부 기능을 검토하여 다른 접근법보다 더 일관성으로 결과의 한계를 설정할 수 있습니다. 함수는 조각 기능으로 간주됩니다. 일반적으로 제안 된 방법은 Intlab (Matlab 도구 상자) 접근법에 의해 얻은 것보다 상당히 좁은 간격을 생성했습니다. 그러나 우리의 방법은 상당히 많은 수의 반복이 필요하다는 것이 분명합니다.
관련 연구
동일한 저널에 실린 기사에서“간격 연장선으로 재귀 함수의 신뢰할 수없는 컴퓨터 시뮬레이션 감지”, https://doi.org/10.1016/j.amc.2018.02.020에 발표 된 우리는 이러한 아이디어를 사용하여 컴퓨터의 긴 시뮬레이션이 현재 소프트웨어 및 하드웨어에 유효하지 않다는 이전 결과를 보여주었습니다. 우리는 또한 오류 전파를 악용하여 "반올림 모드를 사용하여 가장 큰 양의 lyapunov 지수의 계산"과 https://doi.org/10.1016/j.chaos.04.032.
미래 방향
우리는 컴퓨터가 과학과 기술을 개발하기위한 놀라운 도구라고 확신합니다. 그러나 우리는 또한 그들이 함정을 분석하고 피할 수 있도록 그들이 작동하는 방식을 이해해야한다고 확신합니다.
이러한 결과는 최근 저널 Applied Mathematics and Computation에 발표 된 부분적인 접근 방식을 사용하여 Maps의 interval 컴퓨팅주기 궤도라는 제목의 기사에 설명되어 있습니다. 이 작업은 Erivelton G. Nepomuceno, Heitor M. Rodrigues Junior 및 Samir A.M.에 의해 수행되었습니다. 상 연방 대학교의 마틴은 마리 보르 대학교 (Beihang University of Maribor) 대학교 (University of Maribor)의 Matjaž Perc, Matjaž Perc, Maribor 대학의 Mitja Slavinec.
