
최근에 촉촉한 회전 얕은 물 모델에서 Rostami &Zeitlin [1]에 의해 최근에 꾸준하고 오래 지속되며 천천히 동쪽으로 움직이는 대규모 일관성 트윈 사이클론, 소위 "적도 모형"이보고되었다 [2, 3]. 이 개선 된 모델은 이미 지구와 다른 행성에서 제트기와 소용돌이의 안정성에 대한 연구에 이미 적용되었습니다 [4, 5]. 동쪽으로 전파하는 일부 행성 규모의 시스템은 켈빈 파와 매든-줄리안 진동 (MJO)이다 [6]. 전자는 너무 빠르게 전파되고 (약 50m/s), 후자는 상기 속도가 매우 낮습니다 (약 5m/s)
열대 대기의 수수께끼 중 하나는 MJO의 역동적 인 특성이며, 이는 주기적으로 발생하는 대규모 대량의 대규모 패턴이며, 이는 해상 대륙을 통해 인도양에서 동쪽으로 천천히 움직이며 태평양에서 사망합니다. MJO는 약 반세기 전에 1972 년 Madden과 Julian에 의해 발견되었으며 [6], 그 구조와 특성에 대해 많이 알려져 있지만, 역동적 인 특성은 명확하게 이해되지 않습니다. 특히, MJO 이벤트가 천천히 동쪽으로 움직이는 이유에 대한 문제는 여전히 답이 없습니다. 기후 모델은이를 재현하는 데 어려움이 있습니다 (예 :Kim et al. (2011) [7]. 안정적인 대규모 동쪽으로 움직이는 구조물을 생산할 수있는 적도파의 유일한 종인 Kelvin Waves는 MJO보다 속도가 훨씬 빠릅니다. 준 선형의 단순화 된 MJO 모델이 존재합니다. Majda and Stechman (2009) [8] 또는 본질적으로 비선형 (예 :Haertel et al. (2013) [9], 그들 모두는 본질적으로 수분의 역동적 인 역할에 의존합니다.
MJO의 스케일과 천천히 동쪽으로의 위상 속도를 설명 할 때 대규모 대기 흐름과 촉촉한 대류 사이의 선형 파 상호 작용으로서 MJO를 일반적으로 제시하는 이전의 이론적 연구의 능력은 의문의 여지가있다. 따라서 열대 기상학의 도전 중 하나는 MJO의 역동적 인 특성에 대한 설명입니다. 이 현상의 역학적 기원, 형성 또는 발달에 대한 설명에 대한 합의는 없습니다. Rostami와 Zeitlin의 제시된 적도 모돈이 MJO의 모든 역학적 특징을 설명 할 수 있다고 주장하는 것은 너무 이르다. 그럼에도 불구하고, 그것은 MJO의 가장 건조한 특징을 보여줍니다. 적도, 느린 위상 속도, 하이드로-동력 코 히어 런트 구조, 촉촉한 수렴 영역을 따라 동쪽으로 전파되고 Rostami와 Zeitlin의 Modon은 정확한 솔루션을 보장합니다.
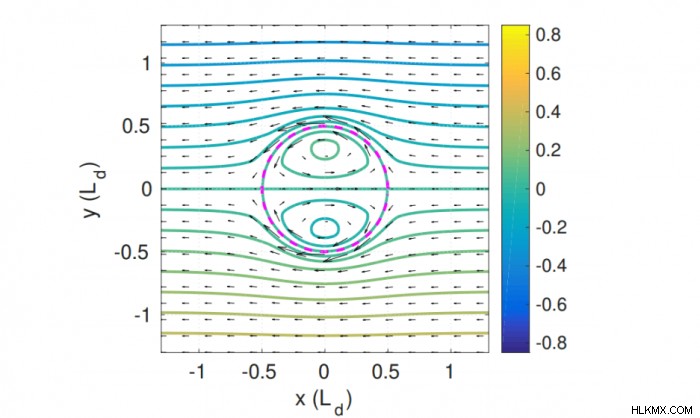
그러나이 문제는 적도를 따라 동쪽으로 천천히 움직이는 "건조한"역학 구조가 존재하는지 여부에 관계없이 MJO 이벤트에 "백본"을 제공 할 수 있습니다. 선형 적도파의 스펙트럼이 잘 확립되어 있으며, 그러한 물체는 반드시 비선형이어야합니다. 중간 율법의 유체 층에 꾸준한 동쪽으로 움직이는 구조가 존재합니다. -평면, 소위 모돈, Larichev and Reznik (1976)에 의해 발견 된 준 지구학 (QG) 방정식의 정확한 쌍극자 솔루션 [10]. 고전적인 모돈은 QG 근사에서 분석적으로 발견되었지만, 컴퓨터 보조 분석에 의해 먼저 나타 났으며, 해당 솔루션이 부모 회전 얕은 물 (RSW) 모델에도 해당 솔루션이 존재한다는 직접적인 수치 시뮬레이션에 의해 보여졌습니다. -평면.
개척 종이에서 Yano와 Tribbia [11]는 MJO가 구형 지오메트리의 그러한 모돈과 관련 될 수 있다는 생각을 내놓았으며 접선 평면에서와 같이 동등한 기압 모돈은 구의 RSW에서 지속된다는 것을 보여 주었다. 적도 베타 평면에서 RSW의 열대 대기의 역학을 이해하기위한 원형 모델. 적도에는 일관된 QG 근사가 없으므로 알려진 Modon 솔루션을 빌릴 수 없습니다.
최근 논문에서 Rostami &Zeitlin이 적용한 직관적 인 접근법은 RSW의 역동적 인 체제이며, 해양학의 장파 근사화 (Gill 1982) [12]는 작은 압력 변화에 해당하고 선두에 서면, 개선 용액을 허용하는 방정식에 해당합니다. 이 준 바로 트로픽 체제는 적도 대기에 대한 비 분산 균형 모델 인 Charney (1963)의 RSW 아날로그입니다. 이 모델의 대규모 열대 운동의 관련성은 척도 및 데이터 분석에 의해 뒷받침됩니다. Rostami와 Zeitlin 은이 정권에서 Modon Solutions를 구성하고 이러한 점근 적 솔루션을 사용하여 전체 RSW 모델로 고해상도 수치 시뮬레이션을 초기화하여 일관된 쌍극 적 정상 동쪽으로 이동하는 구조가 발생하고 지속됨을 보여줍니다. 그런 다음 응축과 증발로 수분을 포함시키는 것은 오랜 일관성을 방해하지 않고 모돈을 향상시키고 특정 대류 패턴을 생성한다는 것을 보여주었습니다.
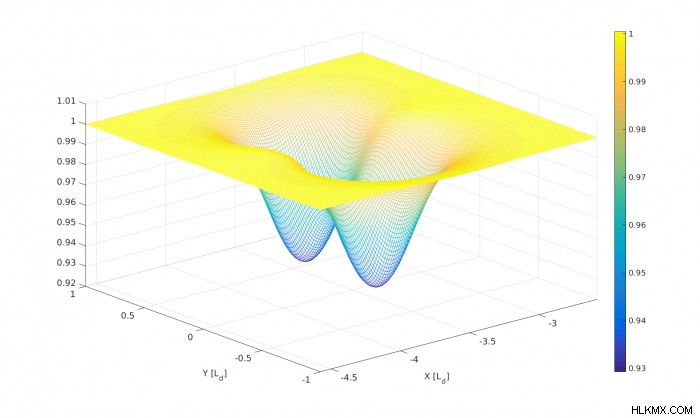
.
참조 :
- m. Rostami와 V. Zeitlin,“적도 탄젠트 평면의 얕은 물에 동쪽으로 이동하는 대류가 강화 된 대체.” J. Phys. 유체의. 31, 021701 (2019). https://aip.scitation.org/action/cookieabest
- m. Rostami와 V. Zeitlin,“개선 된 습한-컨테이션 회전 얕은 물 모델과 허리케인과 같은 소용돌이의 불안정성에 대한 적용,”Q. J. R. Meteorol. 사회 144, 1450 (2018).
https://onlinelibrary.wiley.com/action/cookieabent - m. Rostami와 V. Zeitlin,“회전하는 얕은 물 f 평면 모델에서 소용돌이의 바로 트로픽 및 바로 클리닉 불안정성에 대한 응축 및 잠재 열 방출의 영향.” J. 지구 물리학 및 천체 물리학 적 유체 역학, 111 (1), 1–31 (2016). https://www.tandfonline.com/action/cookiebesent
- m. Rostami, V. Zeitlin, A. Spiga,“토성 북극 육각형의 역학적 특성.” J. Icarus, 297, 59-70 (2017). https://linkinghub.elsevier.com/retrieve/pii/s0019103516305978
- m. Rostami, V. Zeitlin, L. Montabone,“화성의 환상적인 극성 소용돌이의 진화에 대한 공간적으로 불균일 한 당뇨병 효과의 역할.” J. Icarus, 314, 376-388 (2018).
https://linkinghub.elsevier.com/retrieve/pii/s0019103517306073 - r. Madden, P. Julian,“40-50 일의 열대 지방의 글로벌 규모의 순환 세포에 대한 설명.” J. Atmos. 공상 과학. 29, 1109–1123 (1972).
- d. Kim, A. Sobel, E. Maloney, D. Frierson, I. Kang,“AGCM 266 시뮬레이션에서 계절 내 변동성과 평균 상태 바이어스 사이의 체계적인 관계.” J. 기후 24, 5506–5520 (2011).
- a. J. Majda, S.N. Stechman,“열대 계절적 진동의 골격.” PNA, 106, 8417–8422 (2009).
- p. Haertel, K. Straub, A. Fedorov,“Lagrangian 전복과 Madden - Julian Oscillation.” Q. J. Roy. 만났다. 사회 140, 1344–1361 (2013).
- v. D. Larichev와 G. M. Reznik,“2 차원 독방 Rossby Waves”, Dokl. 소련 아카드. 공상 과학. 231, 1077 (1976).
- J.-I. Yano와 J. Tribbia,“열대 대기 Madden-Julian 진동 :강하게 비선형 무료 독방 Rossby Wave?”J. Atmos. 공상 과학. 74, 3473 (2017).
- a. Gill,“대기-해양 역학.” (Academic Press, 1982).
- j. Charney,“열대의 대규모 운동에 대한 메모”, J. Atmos. 공상 과학. 20, 607 (1963).







