물리학의 모멘텀 이해

운동량은 질량을 곱하여 계산 된 파생 수량입니다, m (스칼라 수량), 시간 속도, v (벡터 수량). 이것은 모멘텀이 방향을 가지고 있으며 그 방향은 항상 물체의 움직임 속도와 같은 방향이라는 것을 의미합니다. 운동량을 나타내는 데 사용되는 변수는 p 입니다 . 운동량을 계산하는 방정식은 다음과 같습니다.

방정식

p = mv

운동량의 Si 단위는 초당 킬로그램 타임 미터 또는 kg 입니다. * m / s .

벡터 구성 요소 및 운동량

벡터 수량으로서, 운동량은 구성 요소 벡터로 분해 될 수있다. x 라는 지시 사항이있는 3 차원 좌표 그리드의 상황을보고있을 때 , y 및 z. 예를 들어,이 세 방향 각각에서 발생하는 운동량 구성 요소에 대해 이야기 할 수 있습니다.

p _x = mv _x
p _y = mv _y
p _z = mv _z

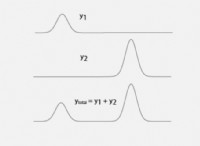
그런 다음 이러한 구성 요소 벡터는 삼각법에 대한 기본 이해를 포함하여 벡터 수학 기술을 사용하여 함께 구성 될 수 있습니다. TRIG 세부 사항에 들어 가지 않고 기본 벡터 방정식은 다음과 같습니다.

p = p _x + p _y + p _z = mv _x + mv _y + mv _z

운동량 보존

추진력의 중요한 특성 중 하나와 물리학을 수행하는 데 중요한 이유는 그것이 보존 된 이기 때문입니다. 수량. 시스템의 총 운동량은 시스템이 어떤 변화를 겪더라도 항상 동일하게 유지됩니다 (새로운 모멘텀 캐리 객체가 도입되지 않는 한)

이것이 중요한 이유는 물리학자가 시스템 변경 전후에 시스템을 측정하고 충돌 자체의 모든 특정 세부 사항을 실제로 알 필요없이 결론을 내릴 수 있기 때문입니다.

함께 충돌하는 두 개의 당구 공의 전형적인 예를 고려하십시오. 이러한 유형의 충돌을 탄성 충돌이라고합니다 . 충돌 후 어떤 일이 일어날 지 알아 내기 위해 물리학자는 충돌하는 동안 발생하는 특정 사건을 신중하게 연구해야한다고 생각할 수도 있습니다. 이것은 실제로 그렇지 않습니다. 대신 충돌 전에 두 공의 운동량을 계산할 수 있습니다 ( p _1i 및 p _2i , 여기서 i "초기"). 이것들의 합은 시스템의 총 운동량입니다 ( p 이라고 부르겠습니다. _t , "T"는 "Total)과 충돌 후 - 총 운동량은 이것과 같고 그 반대도 마찬가지입니다. 충돌 후 두 공의 모멘트는 p 입니다. _1f 및 p _1f , 여기서 f "Final"을 나타냅니다. 이것은 방정식을 초래합니다 :

p _t = p _1i + p _2i = p _1f + p _1f

이러한 모멘텀 벡터 중 일부를 알고 있다면, 결 측값을 계산하고 상황을 구성하는 데 사용될 수 있습니다. 기본적인 예에서, 당신이 볼 1이 쉬고 있다는 것을 알고 있다면 ( p _1i =0) 충돌 후 볼 속도를 측정하고이를 사용하여 운동량 벡터를 계산합니다. p _1f 및 p 2f ,이 세 가지 값을 사용하여 모멘텀을 정확하게 결정할 수 있습니다. _2i 했을 것입니다. 이것을 사용하여 충돌 전에 두 번째 볼의 속도를 결정할 수 있습니다. / m = v .

다른 유형의 충돌을 비탄성 충돌이라고합니다 그리고 이들은 충돌 중에 운동 에너지가 손실된다는 사실 (보통 열과 소리의 형태)이 특징입니다. 그러나 이러한 충돌에서 모멘텀은 입니다 보존, 따라서 충돌 후 총 운동량은 탄성 충돌과 마찬가지로 총 운동량과 같습니다.

p _t = p _1i + p _2i = p _1f + p _1f

충돌로 인해 두 객체가 함께 "고정"되면 완벽하게 비탄성 충돌 이라고합니다. , 최대의 운동 에너지가 손실 되었기 때문에. 이것의 전형적인 예는 총알을 나무 블록으로 발사하는 것입니다. 총알은 나무에서 멈추고 움직이는 두 물체는 이제 단일 물체가됩니다. 결과 방정식은 다음과 같습니다.

m ₁ v _1i + m ₂ v _2i =( m ₁ + m ₂ ) V _f

이전 충돌과 마찬가지로이 수정 된 방정식을 사용하면 이러한 수량 중 일부를 사용하여 다른 수량을 계산할 수 있습니다. 그러므로 당신은 나무 블록을 쏘고, 총에 맞을 때 움직이는 속도를 측정 한 다음, 총알이 충돌하기 전에 움직이는 운동량 (및 속도)을 계산할 수 있습니다.

모멘텀 물리학 및 제 2 법칙

Newton의 두 번째 운동 법칙은 모든 힘의 합계를 알려줍니다 (우리는 이것을 이것을 f라고 부릅니다. sum 일반적인 표기법에는 그리스 문자 시그마가 포함되지만 물체에 작용하는 것은 대상의 질량 시간 가속과 같습니다. 가속도는 속도 변화율입니다. 이것은 시간과 관련하여 속도의 미분입니다. / dt 미적분학 용어로. 기본 미적분학을 사용하면 다음을 얻습니다.