관성은 특정 대중의 몸이 움직일 때 또는 반대로 외부 힘에 의해 정지되기 위해 구입 한 저항의 척도입니다. 관성 또는 물체가 변화에 저항하는 경향은 질량에 따라 다릅니다. 더 무거운 물체는 휴식시 가속하기가 어렵고 가벼운 물체와 비교하여 움직일 때 멈추기가 똑같이 어렵습니다.
물리학의 접두사 '모멘트'는 선형 수량의 회전에 대응하는 데 사용됩니다. 따라서 '관성의 모멘트'는 선형 운동의 질량에 해당하는 회전입니다. ‘I’로 표시됩니다 . 마찬가지로 '힘의 모멘트'는 토크 라고도하는 선형 힘의 회전입니다. .
관성 모멘트를 어떻게 계산합니까?
회전 축과 관련하여 회전 물체의 관성 'I'순간은 질량의 산물과 회전 축에서 거리의 제곱에 의해 주어집니다. 그러나 이것은 특정 각도 속도로 소용돌이 치는 문자열에 부착 된 균일 또는 일반 물체의 경우에만 해당됩니다.
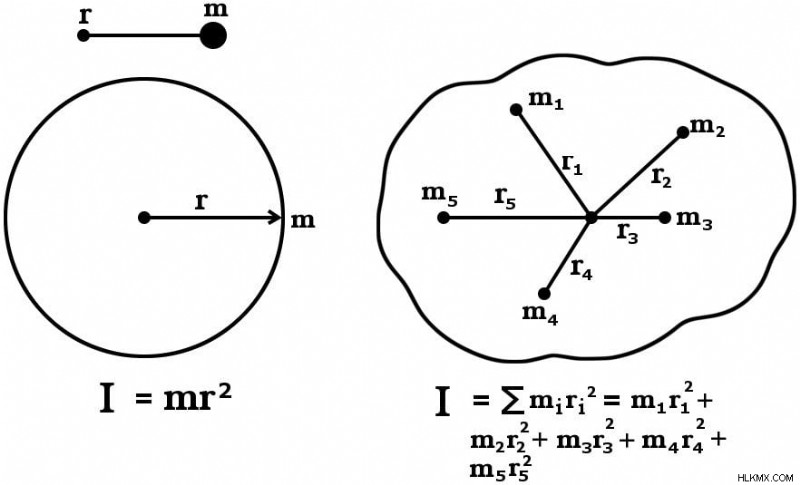
불균일 한 물체의 경우 관성 모멘트는 개별 포인트 의 산물의 합으로 계산됩니다. 질량과 회전 축으로부터의 해당 거리. 이 일반화 된 관계는 모든 시스템의 관성 모멘트를 계산하는 데 사용될 수 있습니다. 어떤 물체는 유사한 포인트 의 집계로 구성 될 수 있기 때문 질량.
다양한 거리에서 질량의 지속적인 질량 분포의 관성 모멘트를 계산하기 위해, 우리는 연속 변수가있는 손재주로 인해 미적분학을 사용합니다.
.
우리는 차동 를 사용합니다 질량 요소, 질량 dm의 무한 덩어리 . 그런 다음 관성의 차동 모멘트는 di =r²dm 입니다. . 관성 모멘트를 계산하려면 ‘I’ 질량 ‘m’, 의 전체 우리는 관성의 차동 모멘트를 요약합니다 di dm 에 의해 기여 표면 전체에. 또는 간단히, 우리는 통합합니다.
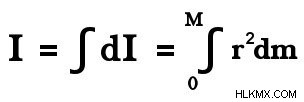
막대 관성의 순간
선형 밀도 λ 가되도록 질량 'M'과 길이 'L'의 막대를 고려하십시오. IS m/l. 회전 축의 위치에 따라로드는 두 모멘트를 보여줍니다. 하나는 축이 막대의 질량 중심을 통해 수직으로 자르면 정확히 중간을 통해; 그리고 둘째, 축이 두 끝 중 하나를 통해 수직으로 위치 할 때.
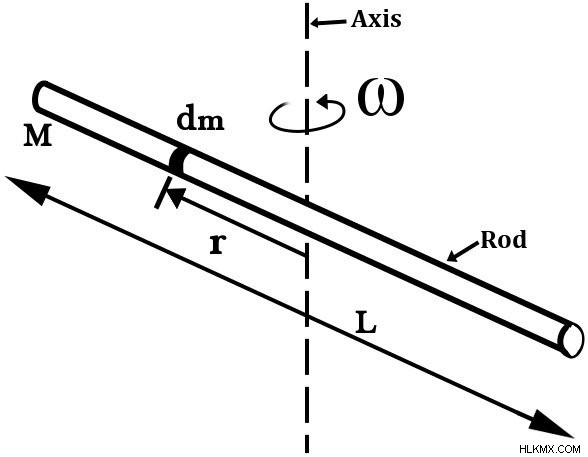
질량 중심을 통한 축
질량 dm의 무한 요소와 유사합니다. 길이 dl 의 무한 요소를 고려하십시오 그것에 해당하는 . 축의 선에 놓여있는 질량 중심에서 원점을 그리면서 우리는 원점에서 끝까지 막대의 거리는 -l/2, 임을 알고 있습니다. 원점에서 다른 쪽 끝로의 오른쪽까지의 거리는 + l/2입니다.
로드가 균일하다고 가정하면, 선형 밀도는 다음과 같은 일정하게 유지됩니다.
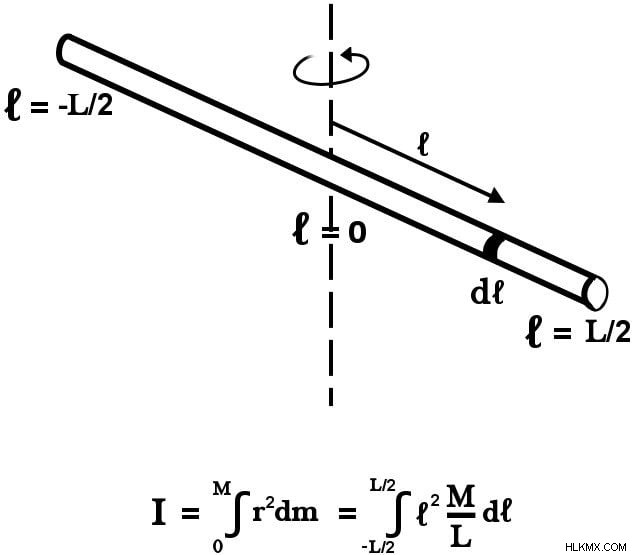
dm 의 값을 대체합니다 관성 모멘트를 계산하기위한 표현에서 우리는 다음을 얻습니다. 
통합 변수는 이제 길이 (dl)이기 때문에 한계는 이전에 묘사 된 M에서 필요한 분율로 변경되었습니다.
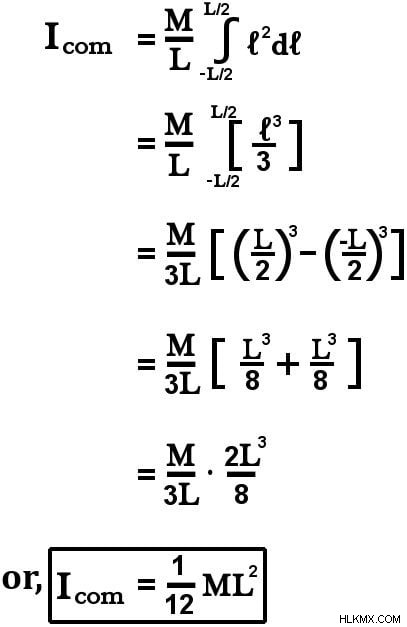
end
를 통한 축축이 끝 중 하나에있을 때 막대의 관성 모멘트를 계산하기 위해, 우리는이 끝에서 원점을 그립니다.
그러나 우리는 현재 다른 한도로 동일한 표현을 사용해야합니다. 축은 끝에 놓여 있기 때문에, 우리가 통합하는 한계는 이제 zero (원점)에서 l (반대쪽 끝)입니다.
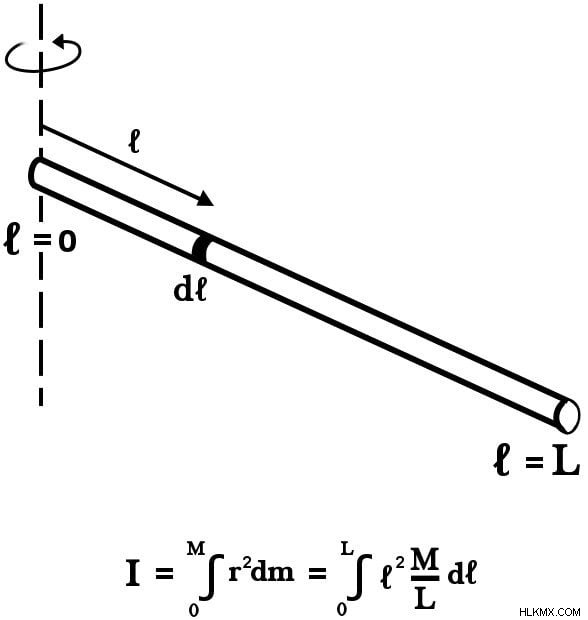
통합 후 :
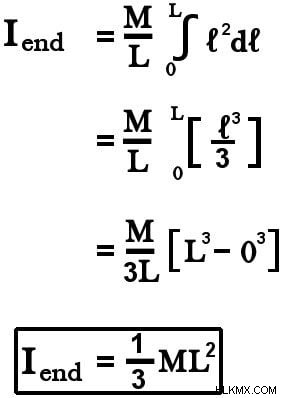
우리는 또한 병렬 축 정리를 사용하여 끝까지 관성 순간에 동일한 결과에 도달 할 수 있습니다. 어느쪽에 따라 :

l (com, end)는 l/2, 입니다 우리는 그것을 발견합니다 :
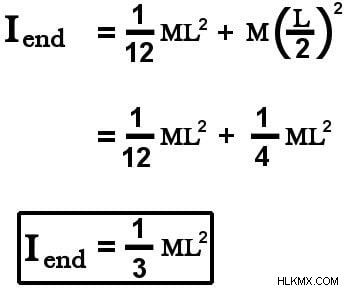
이것은 이전에 파생 된 결과와 일치합니다.