일정한 가속 예제 의이 움직임 방정식 문제는 동전으로 뒤집힌 동전에 대한 최대 높이, 속도 및 비행 시간을 결정하는 방법을 보여줍니다. 이 문제는 수직으로 던져진 물체를 수직으로 해결하거나 키가 큰 건물이나 높이를 떨어 뜨리도록 수정할 수 있습니다. 이 유형의 문제는 모션 숙제 문제의 일반적인 방정식입니다.
문제 :
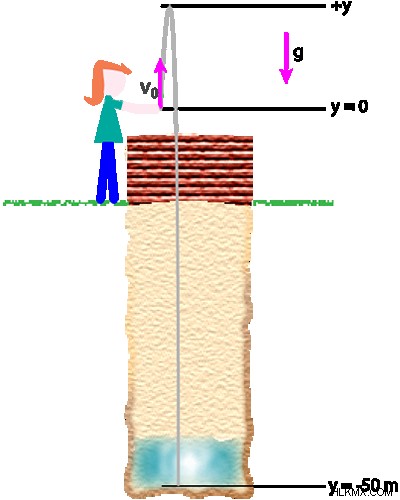
소녀는 동전을 50m 깊이의 소원으로 뒤집습니다. 그녀가 5m/s의 초기 속도로 동전을 위쪽으로 뒤집 으면 :
a) 동전이 얼마나 높아 집니까?
b)이 시점에 도달하는 데 얼마나 걸립니까?
c) 동전이 우물의 바닥에 도달하는 데 얼마나 걸립니까?
d) 동전이 우물의 바닥에 닿을 때의 속도는 얼마입니까?
솔루션 :
발사 지점에서 시작할 좌표 시스템을 선택했습니다. 최대 높이는 포인트 +y이고 웰의 바닥은 -50m입니다. 발사시 초기 속도는 +5 m/s이고 중력으로 인한 가속도는 -9.8 m/s입니다.
이 문제에 필요한 방정식은 다음과 같습니다.
1) y =y 0 + v 0 t + ½at
2) v =v 0 + at
3) v =v 0 + 2a (y - y 0 )
파트 A) 동전이 얼마나 높아 집니까?
동전 비행의 상단에서 속도는 0과 같습니다. 이 정보를 사용하면 위의 방정식 3을 사용하여 상단에서 위치를 찾을 수 있습니다.
v =v 0 - 2a (y - y 0 ))
0 =(5 m/s) + 2 (-9.8 m/s) (y-0)
0 =25 m/s - (19.6 m/s) y
(19.6 m/s) y =25 m/s
y =1.28 m
파트 B) 정상에 도달하는 데 얼마나 걸립니까?
방정식 2는이 부분에 유용한 방정식입니다.
v =v 0 + at
0 =5 m/s + (-9.8 m/s) t
(9.8 m/s) t =5 m/s
t =0.51 s
파트 C) 우물의 바닥에 도달하는 데 얼마나 걸립니까?
방정식 1 은이 부분에 사용할 것입니다. y =-50 m을 설정하십시오.
y =y 0 + v 0 t + ½ at
-50 m =0 + (5 m/s) t + ½ (-9.8 m/s) t
0 =(-4.9 m/s) t + (5 m/s) t + 50 m
이 방정식에는 두 가지 솔루션이 있습니다. 2 차 방정식을 사용하여 찾으십시오.
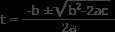
어디
a =-4.9
b =5
C =50
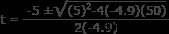
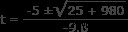
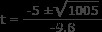
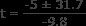

t =3.7 s 또는 t =-2.7 s
부정적인 시간은 동전이 던지기 전에 해결책을 의미합니다. 상황에 맞는 시간은 긍정적 가치입니다. 우물의 바닥까지의 시간은 던져진 후 3.7 초입니다.
Part D) 우물 바닥의 동전 속도는 얼마입니까?
방정식 2는 여기에 도착하는 데 걸리는 시간을 알고 있기 때문에 여기서 도움이 될 것입니다.
v =v 0 + at
v =5 m/s + (-9.8 m/s) (3.7 초)
V =5 m/s - 36.3 m/s
V =-31.3 m/s
우물의 바닥에서 동전의 속도는 31.3 m/s였습니다. 부정적인 부호는 방향이 아래쪽임을 의미합니다.
이와 같은 더 많은 예제가 필요한 경우 다른 일정한 가속 예제 문제를 확인하십시오.
운동 방정식 - 일정한 가속 예제 문제
운동 방정식 - 차단 예제 문제
발사체 모션 예제 문제