에너지 보존 법칙

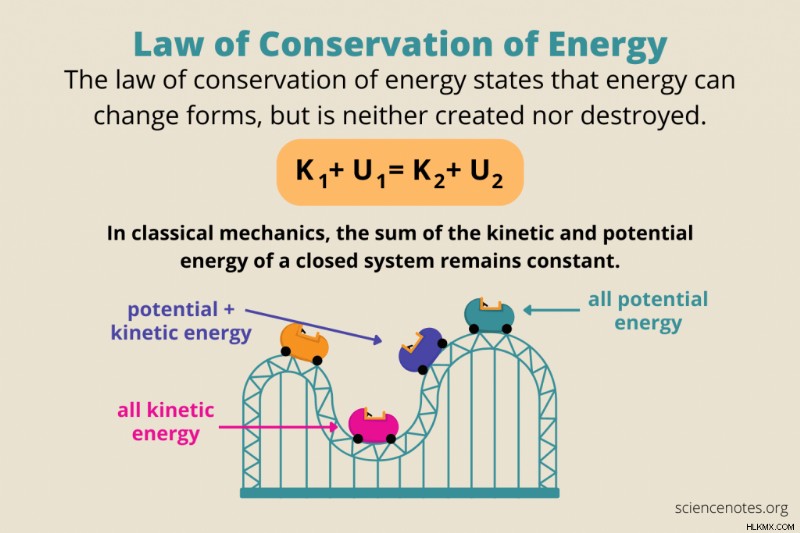
에너지 보존 법칙은 에너지가 형태를 바꿀 수 있지만 분리 된 시스템의 총 에너지는 일정하다고 말하는 물리 법칙입니다. 다시 말해, 에너지는 시간이 지남에 따라 보존됩니다. 에너지 보존 법칙은 열역학의 첫 번째 법칙입니다. 프랑스 수학자이자 철학자 Émilie du Châtelet은 18 세기에 법을 처음 제안하고 테스트했습니다.

공식

에너지 보존 법칙을위한 공식을 작성하는 몇 가지 방법이 있습니다. 가장 일반적인 공식 중 하나는 운동 에너지 (k)와 잠재적 에너지 (U)의 관계를 설명합니다.

k ₁ + u ₁ =k ₂ + u ₂

이 경우 시스템의 총 에너지는 일정하지만 에너지는 전위와 운동 에너지 사이를 전환합니다.

마찰이없는 카트, 스윙, 진자, 공을 던지는 등과 관련된 계산의 경우, 에너지 보존에 대한 또 다른 유용한 형태의 에너지 방정식이 있습니다.

u =mgh; U는 잠재적 에너지 인 경우 M은 질량이고, G는 중력으로 인해 가속이며, H는 높이입니다.
k =½mv; 여기서 m은 질량이고 V는 속도

총 에너지는 잠재력과 운동 에너지의 합입니다 :

e _총 = MGH + ½MV

이 공식은 마찰이없는 물리 문제에 적합합니다. 더 복잡한 방정식은 일부 에너지가 마찰을 통해 열로 전환되는 상황을 포괄합니다.

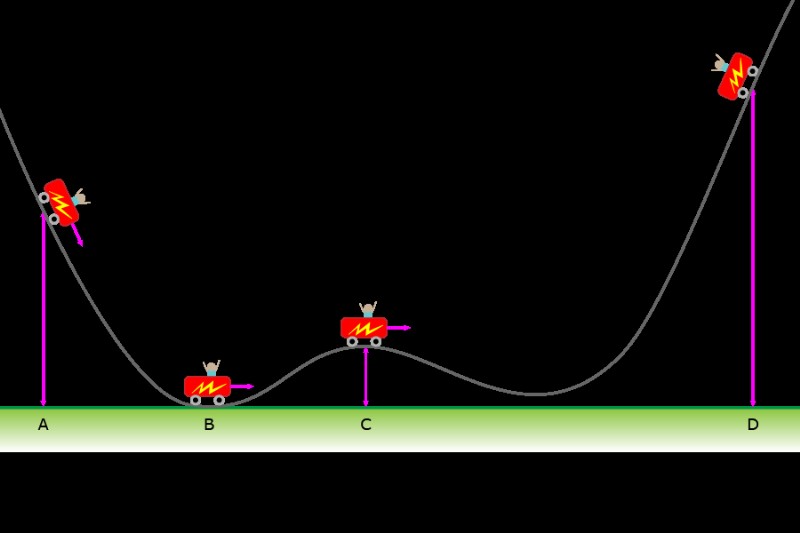
에너지 예제 보존 문제

마찰이없는 트랙을 여행하는 카트와 관련된이 일반적인 물리학 문제로 에너지 보존을위한 공식을 참조하십시오.

에너지 보존 법칙의 또 다른 형태는 시스템의 내부 에너지 (∆E)가 경계 (Q)에 걸친 열 흐름 (Q)과 시스템에서 수행 된 작업 (w).

∆E =Q + W

에너지 보존 법칙의 예

일상 생활에서 에너지 보존 법칙에 대한 많은 사례가 있습니다.

• 스윙에 대한 어린이의 에너지는 잠재력과 운동 에너지 사이의 변화입니다. 스윙의 꼭대기에서 모든 에너지가 잠재력이 있습니다. 스윙의 바닥에서는 모두 운동입니다. 에너지는이 두 지점 사이의 운동 및 잠재적 에너지의 혼합물입니다. 마찰이없는 시스템에서 상단의 잠재적 에너지는 하단의 운동 에너지와 같으며, 이는 다른 지점에서 운동 및 잠재적 에너지의 합과 같습니다.
• 스윙 진 진자는 또한 스윙과 똑같은 동역학과 잠재적 에너지 사이의 전환을 보여줍니다. 물론, 스윙과 진자 예에서 마찰은 역할을합니다. 보존 된 에너지는 실제로 운동 에너지, 잠재적 에너지 및 열 에너지 또는 열의 혼합물입니다.
• 자동차는 화학 에너지 (가솔린)를 운동 에너지로 전환합니다. 여기서 다시, 에너지가 열로 손실되지만 에너지 형태의 합은 일정하게 유지됩니다.
• 사과가 나무에서 떨어지면 잠재적 인 에너지로 시작합니다. 떨어지면서 동역학과 잠재적 에너지가 혼합되어 있습니다. 순식간에 그것은 땅에 닿는다. 모든 에너지는 동역학이다. 잠재력과 운동 에너지의 합은 일정한 가치입니다.
• 손전등은 화학 에너지를 배터리에서 전기 에너지로 변환 한 다음 빛과 열로 변환됩니다.
• 스피커는 전기 에너지를 사운드로 변환하여 또 다른 형태의 에너지입니다.
• 발전기는 기계적 에너지를 전기 에너지로 변환합니다.
• 신체는 화학 에너지를 음식에서 기계 에너지 (움직이는 근육), 다른 화학 에너지 분자 및 열로 전환합니다.
• 폭발 불꽃 놀이는 화학적 잠재 에너지를 운동 에너지, 빛, 열 및 소리로 전환합니다.

고전적인 역학 대 일반 상대성

고전적인 역학에서, 에너지 보존법과 질량 보존 법칙은 두 가지 별도의 법칙입니다. 그러나 그들은 아인슈타인의 유명한 방정식에서 상대성을 결합합니다.

e =mc

이 방정식은 질량이 에너지로 전환 될 수 있으며 그 반대도 마찬가지입니다. 에너지 보존 법칙은 관찰자의 참조가 변하지 않는 한 여전히 사실입니다.

영구 모션 머신

에너지 보존 법의 한 가지 결과는 첫 번째 종류의 영구 운동 기계가 불가능하다는 것을 의미합니다. 이들은 추가 에너지 입력없이 영원히 작동하는 기계입니다. 작동하는 영구 운동은 종이에서 잘 보일지 모르지만 기계의 일부 에너지가 열이 형성되기 때문에 실제 세계에서는 효과가 없습니다. 일반적으로 이것은 마찰에서 비롯됩니다. 따라서 기계를 유지하려면 실제로 지속적인 에너지 입력이 필요합니다.

예외

에너지 보존 법칙은 폐쇄 시스템에 적용됩니다. 때로는 시스템을 정의하거나 분리하는 것이 쉽지 않거나 불가능합니다. 이것은 시스템에 항상 시간 변환 대칭이없는 일반적인 상대성 이론에서 작용합니다. 예를 들어, 에너지 보존이 곡선 시공간 또는 시간 결정에 대해 반드시 정의되는 것은 아닙니다.

참조

• Feynman, Richard (1970). Physics vol i 에 대한 Feynman 강의 . 애디슨 웨슬리. ISBN 978-0-201-02115-8.
• Gibney, Elizabeth (2017). "시간을 결정화하려는 퀘스트". 자연 . 543 (7644) :164–166. doi :10.1038/543164a
• Hagengruber, Ruth (ed.) (2011). émilie du Chatelet :Leibniz와 Newton 사이 . 뛰는 것. ISBN 978-94-007-2074-9.
• Kroemer, 허버트; Kittel, Charles (1980). 열 물리학 (제 2 판). W. H. Freeman Company. ISBN 978-0-7167-1088-2.
• Serway, Raymond A.; Jewett, John W. (2004). 과학자와 엔지니어를위한 물리학 (6th ed.). 브룩스/콜. ISBN 978-0-534-40842-8.