당신이 인명 구조 원이고 누군가가 떠 다니는 데 어려움을 겪고 있다고 상상해보십시오. 책임감있는 인명 구조 원이기 때문에 가능한 빨리 그들에게 가고 싶습니다. 당신은 수영 할 때 매우 빠르지 만 모래에서 더 빠르게 달리기도합니다. 수영 선수에게가는 가장 빠른 경로는 무엇입니까? 그것은 그렇게 들리지 않을 수도 있지만, 유명한 물리학 자 Richard Feynman이 제시 한이 퍼즐은 실제로 빛의 행동과 유사합니다. 10 년 전에 처음 읽었지만, 빛의 여행이 어떻게 저를 붙 잡았는지에 대한 교훈.
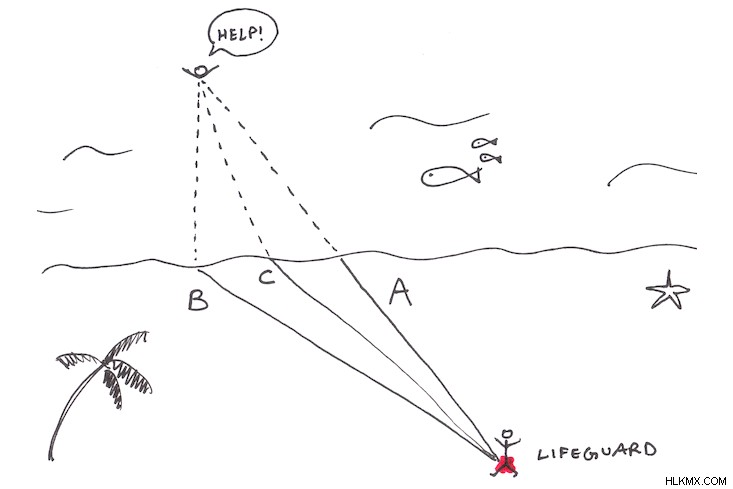
처음에는 직선 (경로 A)이 가장 빠른 경로인지 고려할 수 있다고 생각했습니다. 이것은 실제로 가장 짧은 것이지만 가장 빠르지는 않습니다. 해변을 따라 더 뛰어 다니면 물보다 땅에서 더 많은 거리를 덮을 수 있기 때문에 더 잘할 수 있습니다. 그리고 당신은 육지에서 더 빠르기 때문에 더 적은 시간 안에 도착합니다.
옵션 B가 가장 빠르나요? 모든 선택 중에서이 길은 수영이 가장 적습니다. 그러나 그것은 옳지 않습니다. 지금 더 빨리 움직이지만이 경로는 너무 길고 속도가 느려집니다.
보시다시피, 여기에는 트레이드 오프가 있습니다. Feynman이 말한 것처럼,“ 최소 거리의 경로에는 물이 너무 많습니다. 최소수의 길은 너무 많은 땅을 가지고 있습니다. 최소한 시간의 경로는 둘 사이의 타협입니다. "가장 빠른 경로는 C입니다. A와 B 사이에있는 매우 구체적인 경로
미적분학 학생들은 이러한 종류의 최적화 문제를 해결하는 법을 배웁니다. 그러나 구조 대원은 어떻게해야합니까? 인명 구조 원은 미분을 계산하고 머리에 방정식을 해결하고 있습니까? 나는 그것을 의심한다. 농구 선수가 자유투를 만들기 위해 발사체 운동 법칙을 이해할 필요가없는 것과 같은 방식으로 훈련과 깎아 지른 본능의 조합을 사용한다고 확신합니다. 어쨌든 우리는 수학을 명시 적으로 수행하지 않고 상당히 까다로운 수학 문제에 대한 솔루션을 근사화 할 수 있습니다. (바다 전류와 같은 추가 변수 때문에 실제로 해결하기가 더 어렵습니다.)
이것이 빛과 어떤 관련이 있는지 궁금 할 것입니다. 1657 년 프랑스 변호사와 수학자 피에르 드 페르 마트 (Fermat의 마지막 정리 뒤에 같은 사람)는 빛이 한 곳에서 다른 곳으로 이동할 때 항상 최소한의 경로가 필요하다는 것을 알았습니다. 이상한 의미는 구조 대원이 가능한 한 빨리 어딘가에 도착해야한다면 빛이 어떤 일을 할 것인지 스스로에게 물어봐야한다는 것입니다.
다음은 이것을 이해하는 방법입니다. 레이저 포인터를 가져다가 물 한 그릇에 비추십시오. 빛은 이제 구조 대원과 비슷한 상황에 처해 있습니다. 공기를 통과 할 때 엄청나게 빨리 휘두르면 물 속에있는 동안 물 분자에 계속 부딪 치기 때문에 속도가 느려집니다. 그리고 빛이 무엇을하는지 보십니까? 그녀가 물에 도달했을 때 구조 대원의 길처럼 구부러집니다.

실제로, Snell 's Law라는 공식은 여행하는 재료와 표면에 닿는 각도에 따라 빛이 구부러지는 정확한 각도를 올바르게 예측합니다. 이 공식은 작동하지만 특히 밝히는 것은 아닙니다 (말하면). 올바른 답을 제공하지만 이유 why 를 제공하지 않습니다. 빛이 구부러집니다.
그러나 Fermat은 이것을 보는 다른 방법을 가지고있었습니다. 그는 가벼운 여행을 할 때, 가능한 모든 다른 경로에서 취할 수있는 모든 경로에서 주어진 엔드 포인트에서 가능한 가장 빠른 경로를 선택한다면 어떨까요? 그것이 무엇을 의미할까요? 그리고 그가이 추측의 결과를 해결했을 때, 그는 Old Old Snell의 법칙을 잘 발견했습니다. Fermat의 추측에 완벽하게 맞습니다 빛의 관찰 된 행동으로.* 여기에는 빛의 독특한 행동에 대한 현명한 설명, 즉 광기에 숨겨진 방법이있었습니다.
그리고 그것은 가벼운 구부러진 방법에 관한 것이 아닙니다. Fermat의 최소한의 원리는 또한 빛이 거울에서 대칭 적으로 바운스 한 이유, 왜 안경의 렌즈에 왜 모양이 있는가, 또는 접시 안테나가 포물선 인 이유를 설명합니다. (Feynman 자신의 깔끔한 응용 프로그램에 대해 텍스트 또는 비디오로 배울 수 있습니다.)
Fermat의 아이디어가 당신에게 조금 이상하게 들리면, 당신은 혼자가 아닙니다. Fermat 시대의 Light에 대한 주요 전문가 중 한 명인 Claude Clerselier는 다음을 썼습니다.
Fermat의 원칙은 원인이 될 수 없습니다. 그렇지 않으면 우리는 자연에 대한 지식을 기반으로 할 것이기 때문입니다. [자연]은 선택의 여지없이, 선택없이, 필요한 결정에 의해 행동합니다.
.Fermat의 아이디어에 대해 모든 사람을 괴롭힌 것은 기관이 기관을 요구하는 것 같았다는 것입니다. 빛이 어떻게 선택할 수 있습니까? 길? 아마도 어떻게 알 수 있습니까 가장 빠른 경로는 무엇입니까? 어떻게 든 다른 경로를 스니핑합니까? Fermat은 당시에 그것을 몰랐지만 대답은 그렇습니다. Feynman을 넣는 방법은 다음과 같습니다.
최소 시간의 원칙은 자연이 작동하는 방식에 대한 완전히 다른 철학적 원리입니다. 우리가 한 가지 일을 할 때, 다른 일이 발생하는 등의 인과 관계라고 말하는 대신, 우리는 상황을 설정하고 빛이 가장 짧은 시간, 극단적 인 시간을 결정하고 그 길을 선택합니다. 그러나 그것은 무엇을합니까, 어떻게 알 수 있습니까? 근처의 길을 냄새 맡고 서로 대항하여 확인합니까? 대답은 그렇습니다. 어떤 식 으로든
입니다"Quantum Eraser"와 같은 시연에서 Light의 기괴한 양자 행동과 마찬가지로, 이것은 물리학이 인간 크기 척도에서 어떻게 작동하는지에 대한 직관적 인 이해로 제곱하기가 매우 어렵습니다. 그러나 실험은 안경과 포물선 요리의 지속적인 유용성과 함께 빛이 효과적으로 스니핑하고 가능한 가장 짧은 경로를 선택한다는 것을 확실하게 확인합니다.
.최근에 나는 구조 대원과 빛과 같은 속임수를 당기는 동물의 두 층을 발견했습니다. 그들이 이것을하는 방법은 미스터리입니다.

첫 번째 생물은 Tim Pennings라는 수학 교수와 함께 살았던 Elvis라는 웨일스 어 코르기 개입니다. 팀은 미시간 호수의 해안에서 엘비스와 놀았습니다. 그는 Elvis가 가장 좋아하는 테니스 공을 물에 던져 넣었고 Elvis는 다트를 벗고 가져올 것입니다.
이 Fetch 게임에서 Tim은 Elvis가 흥미로운 일을하고 있음을 알았습니다. 그가 공을 물에 던졌을 때, 엘비스는 서핑으로 뛰어 들어 전체 길을 수영하지 않았습니다. 직접 경로를 선택하는 대신 엘비스는 일반적으로 해안을 따라 달려 가서 특정 시점에서 갑자기 물로 바뀌어 공을 위해 수영을했습니다.
이것은 Tim의 마음에 질문을 제기했습니다. Elvis가 최소한의 길을 밟고 있다면 어떻게해야합니까? 수학 교수 인 Tim은 앉아서 미적분학을 사용하여 테니스 볼 문제에 대한 최적의 솔루션을 해결했습니다. 그런 다음 그는 자신의 아이디어를 테스트하기로 결정했습니다.
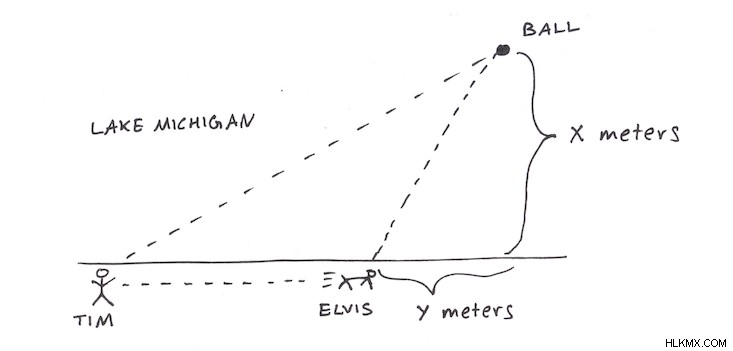
그는 미시간 호수에서 개와 함께 하루를 보냈으며 테니스 공을 물에 던져서 엘비스가 해안을 따라 달리는 거리와 공이 얼마나 멀리 여행했는지를 측정했습니다. 이러한 데이터 포인트 (위 그림의 x 및 y 값)를 수집 한 후, 그는 그것들을 그렸습니다. 이러한 데이터 포인트와 함께 그는 또한 아래 직선으로 표시된 최적의 궤적을 그렸습니다.
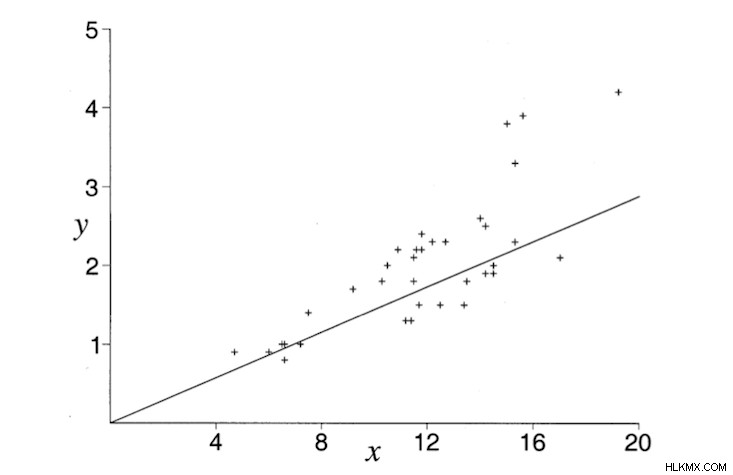
그리고 실제로, Elvis는 최적의 경로를 찾는 데 꽤 좋은 일을했습니다. 그는 가장 짧은 경로 대신 가장 빠른 경로를 지속적으로 선택했습니다! 수학적 모델은 물에 해류가없고, 엘비스가 피곤하지 않고 일정한 속도로 달리고 수영하는 많은 단순화 된 가정을 만들어야한다는 것을 명심하십시오. 실제로 Elvis는 모델에 의해 예측 된 솔루션보다 훨씬 빠를 수 있습니다.

Tim은 Elvis의 속임수에 충분한 인상을 받았습니다. Tim은“엘비스는 미적분학을 알지 못한다… 더 진지하게, 그는 계산을 수행하지는 않지만 Elvis의 행동은 자연이 종종 최적의 해결책을 찾는 어수선한 방법의 예입니다.”
.(그건 그렇고, Elvis는 유일한 송곳니 최적화 제이저가 아니 었습니다. 다른 논문에서 두 명의 수학자 두 명은 여성 래브라도 인 살사도 프랑스에서 호수를 따라 잡을 때 가장 적은 시간의 길을 선택했다고 확증했습니다. 수학자의 개는 소유자의 능력 중 일부를 채택했을까요?)
.이 어수선한 능력을 가진 두 번째 생물은 세계에서 가장 침략적인 종 중 하나입니다. . 개미는 여행 할 때 페로몬의 흔적을 남겨서 서로 탐색하는 데 도움이되며, 시간이 지남에 따라이 트레일은 음식 소스에서 둥지로 직선으로 수렴합니다. 이 작은 사람들은 자연 최적화 자이며, 꽤 복잡한 미로에서 가장 짧은 길을 찾을 수도 있습니다.
그러나 ANT가 구조 대원 딜레마에 직면했을 때 어떤 일이 발생하는지 실제로 연구하지 않았습니다. 매끄러운 표면에서 (빠른 곳)에서 실제로 끈적 끈적한 표면 (느린 곳)으로 이동하면 직접 경로를 선택하거나 최소한의 경로를 선택합니까?
따라서 유리 표면과 거친 녹색 펠트 표면을 사용하여 모래와 물과 유사한 연구 그룹이이를 테스트하기 시작했습니다. 그들은 개미 트레일이 직접 경로보다 가장 빠른 경로에 훨씬 더 가깝다는 것을 발견했습니다. 빛과 구조 원과 마찬가지로이 개미는 거리가 아닌 시간을 최소화하는 것처럼 보였습니다.

그러나 그들은 어떻게 그것을합니까? 분명히 그들은 수학을하지 않습니까? 연구원들은 아마도 운이 좋으면 일부 개미가 더 빠른 경로로 길을 잃고 더 효율적이기 때문에 이러한 경로는 주요 경로가 될 때까지 강화 될 것이라고 제안했습니다. 그러나이 개미들이 구조 대원의 딜레마를 어떻게 해결하는지 아무도 모릅니다. 여전히 열린 질문입니다.
진화는 물론 최적화 제이저이며, 유전자 풀에서의 표현이 증가함에 따라 보상 효율성입니다. 영리하고 효율적인 전략은 가장 큰 보상을 얻을 것입니다. 아마도 우리에게 매우 다른 생물들이 매우 다른 수단을 통해 같은 속임수에 도달한다는 것은 놀라운 일이 아닙니다. 그래서 다음에 집으로 돌아가는 가장 빠른 길을 찾으려고 교통 체증에 갇혀있을 때, 개미, 개, 심지어 빛으로부터 교훈을 얻어야 할 것입니다.
.
각주
*Fermat의 원칙에 대한 현대의 진술은 빛이 경로 길이의 작은 변화가 여행 시간에 영향을 미치지 않도록 경로를 선택한다는 것입니다. 대부분의 경우, 이것은 최소한의 경로로 줄어 듭니다. Feynman의 강의는 이것에 더 많은 것을 가지고 있습니다.
미적분학 된 독자의 경우 :Perruchet과 Gallego의 위의 논문은 개가 전체 궤적에 대한 예지가 필요없이 개가 경로를 최적화하기 위해 따라갈 수있는 영리한 규칙을 고안합니다. 흥미로운 읽기입니다. 그리고 다음은 Snell의 법칙에 도달 할 수있는 방법과 Fermat의 원칙으로부터의 성찰 법칙에 대한 파생입니다.
참조
Feynman, Richard Phillips. Qed :이상한 빛과 물질의 이상한 이론 . 프린스턴 대학 출판부, 2006.
Pennings, Timothy J.“개가 미적분학을 알고 있습니까?” College Mathematics Journal 34.3 (2003) :178-182.
Perruchet, Pierre 및 Jorge Gallego. "개는 최적화보다는 관련 요금을 알고 있습니까?" College Mathematics Journal 37 (2006) :1.
Oettler, Jan, et al. "Fermat의 최소 시간 원칙은 기판 경계에서 개미 트레일의 굴절을 예측합니다." plos one 8.3 (2013) :E59739.
온라인으로 무료로 제공되는 Feynman 강의에서 가장 적은 시간의 원칙에 관한 장.
Aatish Bhatia는 최근 물리학 박사입니다. 프린스턴 대학교에서 과학과 공학을 더 많은 사람들에게 가져 오기 위해 일합니다. 그는 수상 경력에 빛나는 과학 블로그의 경험적 열심을 쓰고 트위터에 @aatishb입니다.
Watch :Blackhole Finding Stephen Hawking은 1 년 전에 Richard Feynman에 의해 발견되었습니다.
 천체 물리학 자 및 소설가. " Data-Credits =””Style =“width :733px”>
천체 물리학 자 및 소설가. " Data-Credits =””Style =“width :733px”>
이 고전적인 사실 So Romantic Post는 원래 2014 년 3 월에 출판되었습니다.







