로직 게이트는 입력이 둘 이상인 전자 회로이지만 특정 입력 조합에 대해서만 발생하는 하나의 출력입니다. 3 가지 기본 논리 게이트가 있습니다. 이 게이트를 결합함으로써, 우리는 두 가지 조합 게이트, NAND 및 NOR을 개발할 수 있습니다. 그것들을 모든 디지털 회로의 범용 빌딩 블록이라고합니다. 이것은 NAND 나 게이트 만 반복적으로 사용하면 모든 게이트의 논리 기능을 얻을 수 있기 때문입니다.
a 또는 게이트 기능은 또는 게이트의 작동이 아닙니다. 게이트는 입력에 신호가 낮은 경우에만 높은 출력 신호를 제공합니다. NOR 게이트는 NOT 및 OR 게이트를 사용하여 구성됩니다.
a 건물을 건축하거나 NOT 및 OR 게이트를 사용하여
a NOR 게이트 작업은 NOT 및 OR 게이트를 사용하여 실현할 수 있습니다. 첫 번째 작업은 또는 그 결과가 아닌 작동을 사용하여 반전됩니다. 다음 회로 기호는 2 입력 NOR을 보여줍니다.
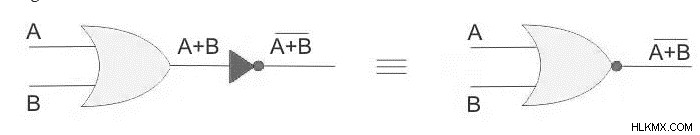
여기서, a와 b는 NOR 배열의 두 입력을 나타냅니다. 모든 입력이 0 인 경우에만 출력은 1의 출력입니다. 다른 모든 입력 조합의 경우 출력이 0입니다.
입력 a
입력 b
a+b
출력 :
0
0
0
1
0
1
1
0
1
0
1
0
1
1
1
0
작업은 다음과 같이 정의 할 수 있습니다. 두 입력이 모두 참 (또는 거짓)이 아닌 경우 출력이 참입니다.
De Morgan의 정리에 따르면 변수의 합의 역수는 취한 개별 변수의 역수의 산물과 동일합니다. 부울 표기법에서는 두 변수의 경우

이것은 NOR 게이트가 역 및 게이트, 즉 버블과 게이트와 동일하다는 것을 나타냅니다.
트랜지스터 사용
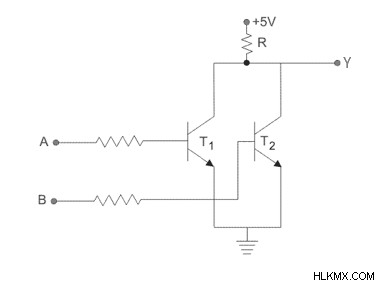
트랜지스터를 사용하여 OR 작업을 실현할 수 있습니다. 아래 그림은 양의 2 입력 로직을 구축하거나 2 개의 병렬 연결 트랜지스터를 사용하는 방법을 보여줍니다.
각 트랜지스터의베이스는 각각 저항을 통해 입력에 연결됩니다. 방출기는지면에 연결되어 있으며 수집기는 +5 볼트의 공급 전압으로 회로에 연결됩니다. 입력 A와 B가 모두 낮 으면 트랜지스터가 차단됩니다. 저항 R을 통과하는 전류가없고, 전압 강하가 없으므로 출력 y가 높습니다. 누군가, A 또는 B 또는 두 입력이 높으면 하나 또는 두 트랜지스터가 포화 상태로 구동되고 출력 Y는 낮아집니다.
만 사용하거나 다른 게이트의 실현
한 유형의 게이트 만 사용하여 논리 회로를 설계하는 것이 종종 편리합니다. De Morgan의 정리를 사용하면 모든 논리 기능을 한 가지 유형의 범용 게이트 만 사용하여 쉽게 구현할 수있는 형태로 표현할 수 있습니다.

Nors, 3 개의 기본 게이트 만 사용하거나 기능하지 않는 기능은 다양한 조합으로 연결하여 생성 될 수 있습니다.
게이트가 아닌 건물
OR 게이트의 작동은 두 입력이 모두 높으면 출력이 높고 다른 모든 조합 (낮은 낮고 낮은 낮은 높이)에 대해 출력이 낮습니다. 이제, A의 부정도 또는 모든 입력이 낮거나 다른 모든 입력 조합 인 경우에만 출력이 적거나 높지 않습니다. 출력이 낮습니다.
만 사용하지 않거나 동등한 것을 구축하려면 입력을 모두 단락시킵니다. 따라서 입력이 높을 때, 즉 a =1, 출력이 낮아지고, y =0이고, 입력이 낮 으면 a =0이면 출력이 높고 y =1은 본질적으로 작동하지 않습니다.
. 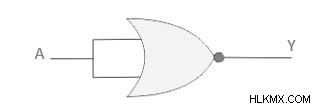
또는 게이트 구축
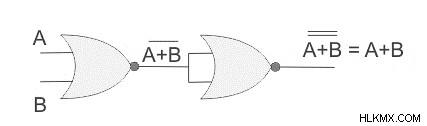
NOR 게이트는 on의 부정입니다. 따라서 거꾸로 된 또는 게이트는 OR 게이트가됩니다. NOR을 반전 시키거나 동등한 또는 게이트를 만들기 위해서는 게이트가 뒤 따르는 것이 효과적입니다. 여기에 사용되지 않은 게이트는 회로를 NORS 만 사용하여 구축해야하므로 다른 나라 게이트에서 실현됩니다. 이 또는 게이트의 논리 회로는 다음과 같습니다.
건물 및 게이트
2 입력의 작동은 다음과 같이 주어질 수 없습니다.

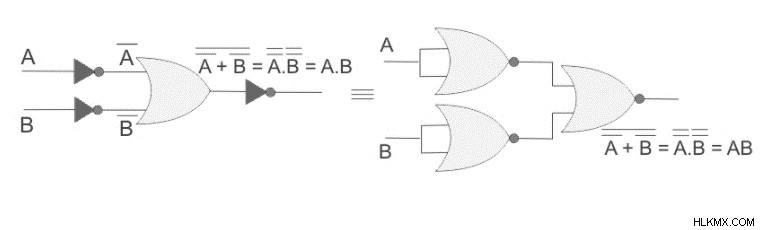
따라서, 우리는 A, 게이트의 입력이 반전되면 출력이 AN 및 게이트가 해당 될 것이라고 추론 할 수 있습니다. NOR 만 사용하여 동등한 것을 만들기 위해, 우리는 동등하지 않은 또는 각각의 입력을 연결합니다. 논리적 등가 회로는 다음과 같습니다.
결론
또한 그 결과 작동이 조합 된 또는 작동이 아닌 보편적 인 게이트도 아닙니다. 우리는 트랜지스터를 사용하여 Not and Or Gate를 사용하거나 구성하거나 구성 할 수 있습니다. NOR 게이트의 출력은 모든 입력이 낮은 경우에만 높습니다. 다른 모든 입력 조합의 경우 출력이 낮습니다. 따라서, A의 작동은 OR의 부정이다. 우리는 모든 기본 논리 연산만을 사용하여 게이트만을 사용하여 실현할 수 있기 때문에 보편적 인 게이트로 간주됩니다.