고조파 진행 또는 고조파 시퀀스는 산술 진행 항의 역수를 선택하여 얻습니다. 이 용어는 다음 형식으로 존재합니다. 1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), 1/(a + 4d), 1/(a + 5d)… 1/(a + (n - 1) d). AP, 즉 산술 진행과 마찬가지로 N 번째 항은 계산할 수 있습니다. 고조파 시퀀스에 속하는 N 용어의 총계입니다. 고조파 진행과 고조파 평균 개념은 수학, 비즈니스, 물리학 및 기타 여러 분야에 널리 적용됩니다. 또한 여러 공식과 예제가 있습니다.
정의
고조파 진행은 AP의 역수를 취하는 과정, 즉 산술 진행 용어를 취할 수 있습니다. 제공되는 AP의 용어는 다음과 같습니다. a, a + d, a + 2d, a + 3d, a + 4d,… 그러면 고조파 시퀀스 또는 고조파 진행 용어가 될 것입니다. 1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), 1/(a + 4d), 1/(a + 5d),… 여기서‘a’는 초기 용어이며‘d’는 공통 차이가됩니다. ‘A’와‘D’에는 0이 아닌 값이 포함되어 있습니다. 특히, 일련의 고조파 진행은 무한한 특성을 가지고 있습니다.
LIRE의 기울기 탑
거친 탑은 고조파 진행의 완벽한 예입니다. 동일한 측면을 갖는 큐브 클러스터가 서로 위에 배치되어 가능한 한 옆으로 또는 옆으로 거리를 얻습니다. 블록의 배치는 1 방향 거리에서 수행됩니다. 1/2, 1/4, 1/6, 1/8, 1/16,… 서로 일대일. 또한, 위에 주어진 쌓인 배열의 동기는 무게 중심이 잘 유지되고 스택이 무너지지 않도록 최대한의 옆 거리를 얻는 것입니다.
고조파 진행의 공식
다음은 고조파 진행에 관한 다양한 계산에 유용한 공식입니다 :
고조파 진행의 n 번째 용어
그것은 AP의 n 번째 항의 상호라고합니다. Harmonic Progression의 N 번째 항은 기본적으로 'D'의 'N - 1'시간, 즉 공통 차이를 포함하여 첫 번째 용어에 속하는 전체 요약 상호입니다. 또한 N 번째 용어는 고조파 진행에 속하는 모든 유형의 용어를 찾는 데 도움이됩니다.
고조파 진행 또는 고조파 시퀀스의 n 번째 항 =1/(a + (n - 1) d)
고조파 평균
고조파 시퀀스 또는 고조파 진행에 대해 이야기하는 동안 시리즈에서 원하는 용어가 인접한 용어의 고조파 평균으로 간주 될 수 있습니다.
고조파 평균 =n/[1/a + 1/(a + d) + 1/(a + 2d) + 1/(a + 3d) +…]
2 용어‘a’와‘b’=(2ab)/(a + b)
의 고조파 평균고조파 평균‘a’,‘b’및‘c’=(3ABC)/(ab +bc +ca)
의 고조파 평균· · 고조파 시퀀스 또는 진행 =1d.log (2a + (2n - 1) d2a - d) 1d.log (2a + (2n - 1) d2a - d)
AM, GM 및 HM
의 관계여기서, 우리는 산술 평균 (AM), 기하 평균 (GM) 및 고조파 평균 (HM)에 속하는 제공된 세트와 관련하여 AM, GM 및 HM 간의 관계가 있습니다. 산술 평균은 기하 평균과 고조파 평균에 의해 계속됩니다. ‘AM’은‘GM’보다 크고‘GM’은‘HM’보다 큽니다.
기하학적 평균 제곱은 고조파 평균의 곱셈 결과와 산술 평균의 결과와 동일합니다.
gm2 =hm x am
고조파 시퀀스 응용
고조파 순서는 고조파 평균과 함께 수학, 물리, 공학 및 비즈니스의 다른 영역에서 다양한 응용 분야를 포함합니다. 다음은 고조파 시리즈에 속하는 몇 가지 필수 응용 프로그램입니다.
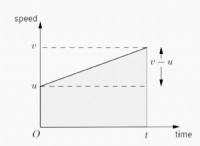
● 2 세트의 동등한 거리 중에서 자동차의 표준 평균 속도는 특정 속도의 고조파 평균을 사용하여 계산할 수 있습니다. 차량의 초기‘D’마일에 대해‘X’미터/시간의 속도가있는 경우 다가오는‘D’마일의‘Y’미터/시간이면 전체 거리를 통해 차량은 2 개의 주어진 속도에 대한 고조파 평균과 동등한 평균 속도를 갖습니다. 따라서 여기서 평균 속도는 =(2xy)/(x + y)입니다.
● 물질 혼합물 또는 합금 밀도의 농도는 동일한 중량 및 동등한 중량 비율을 갖는 두 개 이상의 물질을 포함하는 두 가지 이상의 물질을 포함합니다.
● 렌즈의 초점 길이는 길이에서 'u'에 속하는 거리와 렌즈의 주어진 이미지 'v'의 거리에 속하는 거리에 대해 주어진 고조파 평균에 비해 동일합니다. (1/f) =(1/u + 1/v).
● 기하학적으로, 삼각형의 원격에 속하는 반경은 삼각형의 고도에 속하는 고조파 평균의 1/3에 해당합니다.
● 금융 영역에서, 이익 수익의 비율은 개별 구성 요소에 대한 가중치-하모닉 평균 개념의 도움으로 계산할 수 있습니다.
결론
고조파 진행 예에 대한 노트는 고조파 진행 또는 고조파 서열이 산술 진행의 역수를 취하는 과정과 함께 이루어진다는 결론을 내립니다. 더욱이, 고조파 진행의 개념은 수학, 비즈니스, 물리학 및 기타 여러 분야와 같은 영역에서도 동시에 광범위하게 받아 들여집니다. 또한, 위에서 언급 한 모든 분야 및 영역에 유용한 수많은 고조파 진행 예와 공식이 있습니다. 특히,이 분야에는 고조파 진행 사례의 중요성도 있습니다.