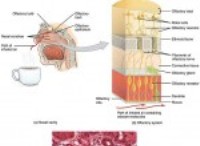
선형 밀도 선형 전하 밀도와 함께 과학 및 공학에 사용되는 두 가지 도구가 있습니다. 수량의 특성의 길이 당 단위는 선형 밀도 라고합니다. . 선형 질량 밀도는 단위 길이로 분포 된 질량의 값이며 선형 전하 밀도는 과학 및 공학 분야에서 사용되는 단위 길이의 전하 값입니다. 따라서 각 분야에서의 중요성을 정의합니다. 단일 치수에 따른 1 차원 물체의 특성 및 3 차원 양의 밀도는 선형 밀도 를 사용하여 결정될 수 있습니다. .
선형 밀도의 치수 공식
선형 밀도의 치수 공식은 [M1L-1T0]으로 작성 될 수 있습니다.
잠열의 치수 공식의 파생 :
선형 밀도 (ρ) =(질량). 1 / (길이)
(ρ) =m / l… (i)
- 치수의 질량 공식 :
[M1L0T0]… (ii)
- 길이의 치수 공식 :
[M0L1T0]… (iii)
방정식 (ii) 및 (iii)의 값을 식 (i)에 넣습니다.
따라서 선형 밀도 =(질량). 1 / (길이)
ρ =[M1L0T0]. [M0L1T0] -1 =[M1L-1T0]
따라서 선형 밀도 치수 적으로 :
로 표시 될 수 있습니다[M1L-1T0]
치수 분석
치수 분석은 관계를 확인하기 위해 물리 수량의 차원을 결정하는 과정입니다. 이 치수는 수치 배수 및 상수와 관련이 없으며, 세계의 모든 양은이 7 가지 기본 차원의 함수로 표현 될 수 있습니다.
치수 분석은 치수와 측정 단위를 사용한 물리적 수량 간의 관계를 연구합니다. 치수 분석은 동일한 단위를 유지하기 때문에 중요합니다. 수학적 계산을 효율적으로 수행 할 수 있습니다.
단위 변환 및 치수 분석
치수 분석을 요인 레이블 방법 또는 단위 계수 방법이라고도합니다. 변환 계수를 사용하여 동일한 단위를 얻습니다. 진술을 설명하려면 3 킬로미터를 구성하는 미터가 있는지 알고 싶다고 가정 해 봅시다.
우리는 1000 미터가 1km와 같다는 것을 알고 있습니다. 따라서 3km는 300 미터의 3 × 1000 미터에 해당합니다. 이 경우 변환 계수는 1000 미터입니다.
물리적 방정식의 정확성을 확인하기위한 도구로서의 차원 분석
- 시간이 속도/거리 또는 거리/속도와 같은지 확실하지 않다고 가정합니다.
- 방정식의 양쪽의 치수를 비교하여 확인할 수 있습니다.
- 우리는 방정식의 각 측면의 기본 단위로 두 방정식을 줄임으로써 이것을 얻습니다.
- 그러나 차원 분석을 사용하여 방정식의 차원없는 상수를 결정할 수 없다는 점에 주목할 가치가 있습니다.
결론
길이 단위당 모든 물체의 특성 특성을 선형 밀도 라고합니다. . 밀도의 농도가 동일하면 균일 한 선형 밀도; 라고합니다. 그리고 그것이 불규칙하다면, 특성의 계산은 힘들어집니다. 물체의 밀도는 파도의 속도에 영향을 미칩니다. 즉, 밀도의 농도가 높으면 파동 속도는 느리고 그 반대도 마찬가지입니다. 따라서 역 비례의 원리를 따릅니다. 선형 밀도 단위 길이 측정 인 반면 표면 밀도는 모든 수량의 특성의 단위 부피 측정입니다.