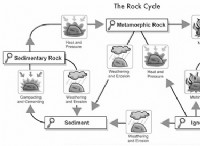
1. 복잡한 시스템 단순화 : 현실 세계는 복잡한 상호 작용으로 가득합니다. 수학적 모델은 현상을 유발하는 주요 변수와 관계에 중점을 두어 불필요한 세부 사항을 추상화 할 수 있습니다. 이 단순화를 통해 패턴을 쉽게 식별하고 다른 요인이 시스템에 어떤 영향을 미치는지 이해할 수 있습니다.
2. 예측 : 모델을 통해 시스템이 다른 조건에서 어떻게 작동하는지 예측할 수 있습니다. 이것은 가설을 테스트하고 실험을 설계하며 미래의 결과를 예상하는 데 도움이됩니다. 예를 들어, 기후 모델은 온실 가스 농도의 변화가 전 세계 온도에 어떤 영향을 줄 수 있는지 이해하는 데 도움이됩니다.
3. 관계를 정량화하십시오 : 수학적 모델은 정확한 방식으로 변수 간의 관계를 표현합니다. 이를 통해 다른 효과의 강도를 정량화하고보다 정확한 예측을 할 수 있습니다. 예를 들어, 뉴턴의 중력 법칙은 질량과 거리에 따라 두 물체 사이의 매력의 힘을 정량화합니다.
4. 복잡한 현상 시각화 : 모델을 사용하여 추상 개념을 이해하는 데 도움이되는 시각화를 만드는 데 사용할 수 있습니다. 예를 들어, 3D 분자 모델을 통해 구조를 시각화하고 서로 상호 작용하는 방법을 이해할 수 있습니다.
5. 테스트 가설 : 수학적 모델은 다양한 시나리오를 시뮬레이션하고 결과를 관찰하여 가설을 테스트하는 데 사용될 수 있습니다. 이를 통해 현상에 대한 우리의 이해가 경험적 관찰과 일치하는지 확인할 수 있습니다.
다음은 다양한 과학 분야에서 수학적 모델이 어떻게 사용되는지에 대한 몇 가지 예입니다.
* 물리학 : 모델은 운동, 중력, 전기, 자기 등을 설명하는 데 사용됩니다.
* 화학 : 모델은 화학 반응, 분자의 거동 및 재료의 특성을 이해하는 데 사용됩니다.
* 생물학 : 모델은 인구 역학, 질병 확산 및 생명의 진화를 연구하는 데 사용됩니다.
* 생태학 : 모델은 종과 환경 사이의 상호 작용을 이해하는 데 사용됩니다.
* 천문학 : 모델은 별, 은하 및 우주의 형성과 진화를 이해하는 데 사용됩니다.
중요한 참고 : 수학적 모델은 강력한 도구이지만 현실의 단순화라는 것을 기억하는 것이 중요합니다. 그들은 완벽한 표현이 아니며 한계가 있습니다. 모델의 정확도는 데이터의 품질과 구조의 가정에 따라 다릅니다. 그럼에도 불구하고, 수학적 모델은 자연 세계를 이해하고 탐구하는 데 필수적입니다.