다음은 신체적 중요성에 대한 고장입니다.
1. 미세 및 거시적 특성 연결 :
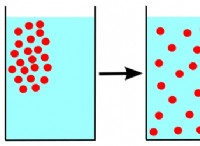
* 확산 계수 (d) : 이것은 거시적 특성으로, 임의의 움직임으로 인해 입자가 용액에 얼마나 빨리 퍼지는지를 설명합니다. m²/s로 측정됩니다.
* 이동성 (μ) : 이것은 미세한 특성으로, 입자가 외부 힘 (전기장과 같은)에 얼마나 쉽게 반응하는지를 설명합니다. m²/(v · s)로 측정됩니다.
Nernst-Einstein 방정식은이 두 가지 겉보기 다른 특성을 연결하여 미세한 거대 거동과 거시적 행동 사이의 기본 연결을 강조합니다.
2. 입자 움직임 이해 :
방정식은 더 높은 확산 계수를 갖는 입자 를 의미한다 또한 더 높은 이동성 를 가질 것입니다 . 이것은 직관적 인 의미가 있습니다.
* 입자가 빠르게 확산되면 자체적으로 많이 움직입니다.
*이 고유 한 움직임은 외부 힘에 더 쉽게 반응하여 더 모바일이 될 것임을 의미합니다.
3. 다양한 분야의 응용 프로그램 :
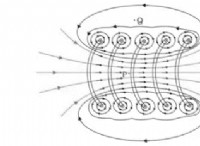
* 전기 화학 : Nernst-Einstein 방정식은 용액, 특히 전기 화학 세포에서 이온 수송을 이해하는 데 중요한 역할을합니다. 용액의 전도도를 이온의 확산 계수와 관련시키는 데 도움이됩니다.
* 솔리드 스테이트 물리학 : 방정식은 반도체 및 기타 재료에서 전하 담체 (전자 또는 구멍)의 움직임을 연구하는 데 사용됩니다.
* 생물학 : 그것은 이온과 분자가 세포막을 가로 질러 어떻게 움직이는 지 설명하고 이러한 움직임이 세포 과정에 어떤 영향을 미치는지 설명하는 데 도움이됩니다.
4. 제한 및 확장 :
* Nernst-einstein 방정식은 이상적인 조건 의 가정하에 도출됩니다. 입자 간의 상호 작용이 무시할 수있는 경우. 실제로, 이러한 상호 작용은 중요하여 예측 된 행동과의 편차를 초래할 수 있습니다.
* 이러한 상호 작용을 설명하기 위해 방정식이 확장되어 실제 시스템을 설명하는 데 더 정확한보다 복잡한 형태가 발생했습니다.
요약하면, Nernst-Einstein 방정식은 다양한 시스템에서 입자의 움직임을 이해하고 예측하는 강력한 도구입니다. 그것은 현미경과 거시적 특성의 기본 연결을 강조하고 다른 분야에서 수송 현상을 연구하기위한 이론적 프레임 워크를 제공합니다. .