가정 :
1. 물리 법칙은 균일 한 운동으로 모든 관찰자에게 동일합니다. 이것은 관찰자의 일정한 속도에 관계없이 물리 법칙이 항상 사실이라는 것을 의미합니다.
2. 진공의 빛 속도 (c)는 광원의 움직임에 관계없이 모든 관성 관찰자에게 동일합니다. 이것은 빛의 속도가 보편적 인 상수임을 의미합니다.
수학적 결과 :
이 가정에서 아인슈타인은 몇 가지 심오한 결과를 유래했으며, 수학적으로 표현됩니다.
* 시간 확장 : 시간 간격은 상대 운동에서 관찰자의 경우 다른 것으로 보입니다. 이것은 고정 관찰자에 비해 고속으로 움직이는 물체의 시간이 속도가 느려짐을 의미합니다. 수학적 :
* t '=t / √ (1 -v² / c²)
* 어디:
* t '는 이동 관찰자가 측정 한 시간 간격입니다.
* t는 고정 관찰자가 측정 한 시간 간격입니다.
* V는 관찰자 간의 상대 속도입니다
* C는 빛의 속도입니다
* 길이 수축 : 객체의 길이는 상대 운동에서 관찰자의 경우 더 짧은 것으로 보입니다. 수학적 :
* l '=l √ (1 -v²/c²)
* 어디:
* l '는 움직이는 관찰자가 측정 한 길이입니다.
* l은 고정 관찰자가 측정 한 길이입니다.
* V는 관찰자 간의 상대 속도입니다
* C는 빛의 속도입니다
* 상대 론적 질량 : 속도가 빛의 속도에 접근함에 따라 물체의 질량이 증가합니다. 수학적 :
* m '=m / √ (1 -v² / c²)
* 어디:
* M '는 상대 론적 질량입니다
* M은 나머지 질량입니다
* V는 물체의 속도입니다
* C는 빛의 속도입니다
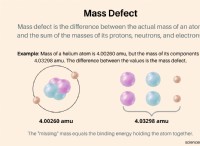
* 질량 에너지 등가 : 에너지와 질량은 동등하여 서로 변환 될 수 있습니다. 이것은 E =Mc² 방정식으로 유명하며, 여기서 E는 에너지, M은 질량이고 C는 빛의 속도입니다.
* Lorentz 변환 : 이들은 시공간 좌표가 상대 운동에서 관성 프레임 사이에서 어떻게 변형되는지를 설명하는 일련의 방정식입니다.
물리학을 통한 표현 :
수학적 표현 외에도 특수 상대성 이론은 물리적 개념과 관찰을 통해 표현됩니다.
* 상대 론적 도플러 효과 : 소스와 관찰자 사이의 상대 운동으로 인해 빛의 빈도가 변합니다. 이 효과는 천문학에서 먼 물체의 속도를 측정하기 위해 사용됩니다.
* 쌍둥이 역설 : 이 사고 실험은 두 쌍둥이에 대한 시간 팽창의 결과를 탐구합니다. 그 중 하나는 고속으로 여행합니다.
* 입자 물리학 : 특수 상대성 이론은 입자 물리학에 대한 우리의 이해와 고속으로 움직이는 입자의 거동에 근거합니다.
전반적으로, 특수 상대성은 공간, 시간, 중력에 대한 우리의 이해를 근본적으로 변화시킨 이론입니다. 그것은 가정, 수학적 방정식 및 물리적 관찰을 통해 표현되어 빛의 속도에 접근하는 속도에서 우주를 이해하기위한 프레임 워크를 제공합니다.