소개
원자 수소와 원자 수가 낮은 수소 유사 이온의 방출 및 흡수 스펙트럼은 Bohr의 수소 원자 모델에 의해 설명됩니다. 원자 상태를 설명하고 원자 내에서 전자 궤도의 양자화를 가정하기 위해 양자 수를 사용한 최초의 모델이었다. 많은 전자 원자를 다루는 양자 역학의 개발은 Bohr의 모델에 의해 도움을 받았습니다.
Bohr 방정식을 어떻게 도출합니까?
- 광자의 에너지가 양자화되고 에너지는 한 궤도에서 다음 궤도로 이동함에 따라 전자의 에너지 변화로 계산됩니다.
방정식 형태로, 이것은 e =hf =ei × ef로 기록됩니다.
- 전자의 궤도는 Bohr의 변형 된 행성 모델에서 양자화됩니다.
Bohr의 모델을 사용하여 쉘의 전자 에너지가 계산됩니다.
e (n) =- 1n2ev
수소 스펙트럼은 전자에 의해 에너지 수준을 변화시키기 위해 광자를 흡수하고 방출하는 전자 측면에서 BOHR에 의해 설명되었다. 여기서 광자 에너지는 EV에서 측정됩니다.
.hν =Δ e =- 13.6 (1nlow2 - 1nhigh2) ev
참고 : Bohr의 모델은 하나 이상의 전자가있는 시스템에서 작동하지 않습니다.
보우의 원자 모델의 가정
- 특정 원형 경로에서 양으로 하전 된 핵 주위의 원자 궤도에서 전자 (음의 하전)
- 이 원형 궤도는 각 궤도 또는 껍질이 에너지를 정의했기 때문에 궤도 껍질로 알려져 있습니다.
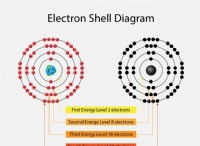
- 양자 번호는 에너지 레벨을 나타내는 정수 (n =1, 2, 3,…)입니다. 가장 낮은 에너지 수준은이 범위의 양자 수에서 n =1이며, 이는 핵 측에서 시작합니다. K, L, M, N…. 껍질은 궤도 n =1, 2, 3, 4…에 주어지고 전자는 가장 낮은 에너지 수준에 도달 할 때지면 상태로 간주됩니다.
- 원자의 전자는 에너지를 얻기 위해 에너지를 얻기 위해 에너지 수준에서 더 높은 에너지 수준으로 이동하고 전자는 에너지를 잃어 에너지 수준에서 에너지 수준이 낮아집니다.
Bohr는이 두 가지 어려움을 극복하기 위해 Bohr의 모델에 대한 세 가지 가정을 도입했습니다.
- 음성 전자는 원형 궤도에서 양성 핵 (양성자)을 궤도에 둡니다. 핵은 모든 전자 조직의 중심입니다. 핵에 결합 된 전자는 가능한 모든 궤도에 접근 할 수 없습니다.
- 허용되는 전자 궤도는 첫 번째 양자화 조건을 만족시킵니다. 전자의 각 운동량은 nth 궤도에서 개별 값 만 취할 수 있습니다 :
ln =nh, 여기서 n =1,2,3
전자의 각 운동량은이 가정에 따라 정량화된다. 첫 번째 양자화 조건은 다음과 같이 공식적으로 작성할 수 있습니다.
mcvnrn =nh
Nth 궤도의 반경과 전자 속도로 각각으로 표시됩니다.
- EN 에너지를 갖는 하나의 궤도에서 EM 에너지를 갖는 다른 궤도로의 전이는 전자에 대해 허용된다. 광자가 원자에 의해 흡수되면, 전자는 고 에너지 궤도로 이동한다. 광자가 원자에 의해 방출되면, 전자는 에너지 궤도로 이동한다. 동시 광자 흡수 또는 방출로 전자 전이는 분할 초에 발생합니다. 두 번째 정량화 기준은 허용 된 전자 전이에 의해 충족됩니다.
hf =en-em
여기서 h는 방출되거나 흡수되는 주파수 f를 갖는 광자의 에너지이다.
- 두 번째 정량화 조건에 따라 수소 원자에서 전자의 에너지 변화가 양자화됩니다.
- 수소 원자의 초기 양자 이론 의이 세 가지 가정을 통해 Rydberg 공식과 Rydberg 상수의 값을 도출 할 수 있습니다. 또한 에너지 수준, 이온화 에너지 및 전자 궤도 크기와 같은 수소 원자의 중요한 특성을 이해하는 데 도움이됩니다.
- Bohr의 모델에는 쿨롱 힘에 노출 된 입자로 전자의 고전적인 설명이 포함되어 있으며, 두 개의 비 고전적 양자화 가정과 함께 뉴턴의 운동 방정식에 순종해야합니다. 고립 된 시스템으로서, 수소 원자는 우리가 고전 물리학에서 알고있는 에너지와 운동량 보존 규칙을 준수해야합니다.
결론
수소 원자의 BOHR 모델은 Rutherford의 모델로 식별 된 일부 간격을 채우는 것을 목표로합니다. Bohr는 원자의 전자가 빛나는 에너지를 생성하지 않고 안정적인 궤도에서 궤도를 돌릴 수 있다고 제안했다. 그러나, BOHR 모델은 단일 전자 종에만 적용됩니다.이 모델은 하나의 양성자와 하나의 전자 사이의 쿨롱 상호 작용 만 고려하기 때문입니다. 하나 이상의 전자가있는 다른 원자 종을 포함하도록 확장 할 수 없습니다. 단일 전자 종에서만 사용할 수 있습니다.