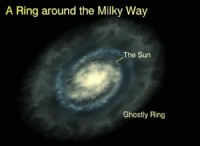
$$ pv =nrt $$
어디:
* P는 대기의 압력 (ATM)입니다.
* V는 리터의 볼륨입니다 (L)
* n은 가스의 두더지 수입니다
* R은 이상적인 가스 상수입니다 (0.08206 L atm / mol k)
* t는 켈빈의 온도입니다 (k)
먼저 C2H2F4 증기의 두더지 수를 계산해야합니다.
$$ n =\ frac {m} {m} $$
어디:
* m은 그램으로 가스의 질량입니다 (g)
* m은 두더지 당 그램의 가스의 몰 질량 (g/mol)입니다.
C2H2F4의 몰 질량은 다음과 같습니다.
$$ m =2 (12.01 \ g/mol) + 2 (1.01 \ g/mol) + 4 (19.00 \ g/mol) =64.06 \ g/mol $$
따라서 C2H2F4 증기의 두더지 수는 다음과 같습니다.
$$ n =\ frac {0.100 \ g} {64.06 \ g/mol} =0.001561 \ mol $$
이제 P, N, R 및 T의 값을 이상적인 가스 법칙으로 대체하여 볼륨을 계산할 수 있습니다.
$$ v =\ frac {nrt} {p} $$
$$ v =\ frac {(0.001561 \ mol) (0.08206 \ l atm / mol k) (295.45 \ k)} {0.0928 \ atm} $$
$$ V =0.404 \ l $$
따라서, 0.0928 ATM 및 22.3 ° C에서 0.100 g의 C2H2F4 증기의 부피는 0.404 L이다.