분자 구조에 대한 아이디어는 화학에 대한 우리의 이해에 필수적입니다. 친숙한 공과 스틱 모델은 단순성이 구체적이고 매력적이지만 설명 가치 측면에서 제한적이거나 오해의 소지가 있습니다. 두 개의 원자 기호 또는 물리적 원자를 연결하는 단순히 선 또는 막대로서 화학 결합의 개념은 그러한 오해의 소지가있는 결과 중 하나입니다.
주어진 화합물의 구조는 X- 선 결정학에 의해 가장 자주 결정되는데, 여기서 원자를 둘러싼 전자 구름에 의한 광자의 산란은 회절 패턴 를 생성한다. 그것은 원자 위치를 드러낸다. 그러나 실험적인 전자 밀도 (ρ ) 분자 구조를 생성합니다. 분자의 특정 모양을 지시하지 않습니다. 즉, 전자의 밀도만으로도 원자를 연결하는 특정 결합의 존재를 고유하게 설명하지 않습니다. 도 1에 도시 된 것과 같은 분자 구조는 근접성과 화학적 원자가의 정상적인 규칙에 기초한 원 자간 연결을 반영한다. 결합 강도와 같은 특성을 추론 할 수 있지만, 궤도 조성과 같은보다 근본적인 특성은 접근 할 수 없습니다.
파동 함수 (ψ)는 양자 역학 (QM)의 기본 개념이며, 이론적으로 주어진 분자에 대한 완전한 설명을 나타냅니다. 파동 함수는 확률 진폭을 나타내며, ψ는 특정 위치에서 입자에 대한 확률 밀도를 제공합니다. 주어진 분자에 대한 Schrodinger 방정식을 해결하는 것은 주어진 핵 구성 (Born-Oppenheimer 근사)에 대한 전자파 기능을 생성하고 최적화 된 구조에 대한 전자식 ψ를 계산하기 전에 핵 좌표를 독립적으로 최적화하는 것을 포함한다. 주어진 전자를 찾을 확률이 90% 인 표면 경계는 궤도로 정의되며, 국소화, 2- 센터 또는 비편성, 다중 센터 결합의 조성을 반영한다. QM 계산의 품질은 일반적으로 X- 선 또는 중성자 회절에 의해 결정되는 실험 구조와 비교하여 평가 될 수있다. 따라서 주어진 결합의 특성, 즉 궤도 구성은 실험 구조가 아닌 이론으로부터 얻어진다.
.최근 논문에서 저자는 ρ 사이에 실제로 관계가 있음을 보여줄 수있었습니다. 그리고 ψ, 즉 아래 방정식 1에 표시된 등가.
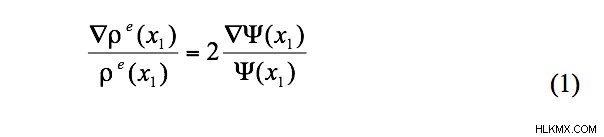wavefunction ψ ( x 1 ) (1)에서는 1- 전자 파도 기능으로 불리며, Schrodinger 방정식의보다 엄격한 모든 전자 ψ에 대한 근사치입니다. 그럼에도 불구하고 (1)의 관계의 유용성은 실험 전자 밀도를 사용할 수 있다는 것입니다. ρ , ψ의 실험 버전을 시각화합니다. 구체적으로 실험적으로 도출 된 플롯
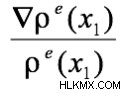
1- 전자파 함수 ψ ( x 의 토폴로지 또는 공간 배열을 표시합니다. 1 ). 분자 [(c 5 나 5 ) OSH 4 (pcy 3 )]] [bf 4 ] 그림 1은 이러한 플롯, 중성자 회절에 의해 결정된 실험 구조 및 Dewar-Chatt-Duncanson 모델로 알려진 이러한 상호 작용에 대한 이론적 설명을 보여줍니다. "실험적"구조가 중앙 금속 원자와 4 개의 수소 사이의 거의 동등한 결합을 나타내는 사실에도 불구하고, ψ ( x 의 플롯 된 실험 버전. 1 ), 또는 ρ ( x 1 ), 금속과 h a 사이의 다른 결합 상호 작용을 나타냅니다. 및 h b , 금속과 h 1 사이에서 관찰 된 것보다 및 H 2 . 기존의 더 현지화 된 본딩 그림과 다르지만, 플롯은 QM 이론에 의해 예측 된 모델과 현저히 유사합니다. 분자의 경우 [Feh 3 (pme 3 )
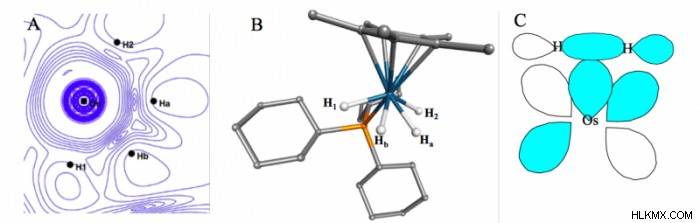
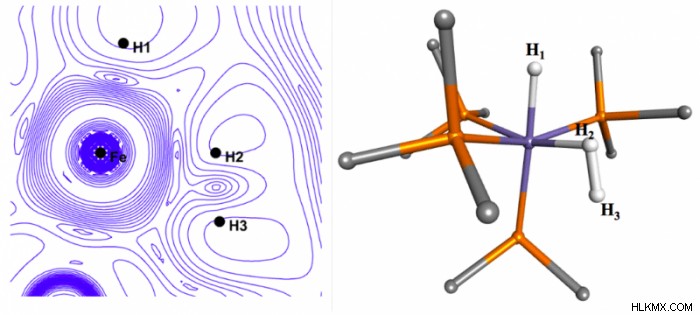ρ 의 플롯을 기반으로 해석 사이의 관점의 차이 ( x 1 ) 그리고 단순히 내부 핵 분리를 기반으로하는 것이 더욱 두드러진다. 후자는 h 2 임을 나타낼 수 있습니다 금속 중심과 다른 수소에 결합됩니다. ψ ( x 1 ), 또는 ρ ( x 1 ),, 결합은 그림 1과 거의 동일하며, QM 이론의 예측과 일치한다는 것을 나타냅니다. 전자 밀도의 사용을 통한 화학 구조 해석은 새로운 것이 아닙니다.
분자에서 원자의 양자 이론으로 알려진 형식은 분자의 전자 밀도 분석을 통한 국소 화학 결합의 아이디어를 검색하는 데 기초하고 있으며, 1998 년 화학 노벨상의 일부는 밀도 기능 이론 (DFT)의 발달에 대한 수상을 받았다. 기본 변수로서 ψ보다는. 하지만. 이 작업은 실험 ρ 을 연결합니다 이론적 ψ를 한 번에 시각적이고 널리 적용 가능하며 희망적으로 유용한 방식으로.
이러한 결과는 최근 저널 계산 및 이론적 화학 에 발표 된 σ- 코디네이션 복합체에서 분자 파 함수를 시각화하는 기사에 설명되어있다. . 이 작업은 St. Edward 's University의 Eamonn F. Healy가 수행했습니다.
참조 :
- Healy, Eamonn F.“σ- 좌석 복합체에서 분자 파 함수를 시각화”, 계산 및 이론적 화학 , 1125 (2018) 128-132.
- 헌터, 제프리. "파도 역학의 조건부 확률 진폭." int. J. Quantum Chem 9 (1975) 237-242.
- Gross, Christopher L. 및 Gregory S. Girolami. “[(C5ME5) OS (L) H2 (H2)+] 복합체의 합성 및 NMR 연구. 용액 및 고체 상태에서 이수소 복합체에 의한 상이한 구조의 채택의 증거.” 유기 금속성 26 (2007) :1658-1664.
- Gusev, Dmitry G., et al. "M (II) 및 M (iv) 복합체의 합성, 구조적 다양성, 역학 및 산도 [MH3 (PR3) 4]+(M =FE, RU, OS; R =ME, ET)." j. 오전. 화학 Soc .119 (1997) 3716-3731.
- Mingos, D. Michael P.“유기 금속 화학에 대한 Dewar의 획기적인 기여에 대한 역사적 관점.” j. 유기농. 화학. 635 (2001) 1-8.
- Bader, Richard FW. "분자의 원자." accs. 화학 해안 18 (1985) 9-15.
