결과적으로 소수와 결정은 공통점이 많습니다. 프린스턴 대학교 (Princeton University)의 연구원들의 새로운 분석에 따르면 숫자 라인에서 소수의 패턴 분포는 특정 크리스탈 유사 재료의 원자 구조에서 발견되는 패턴과 현저히 유사하다는 것을 시사합니다. 간단히 말해서, 숫자 라인의 긴 스트레칭에 걸친 일련의 프라임 시퀀스는 내부 원자 구조를 드러내기 위해 물체의 빛나는 X- 레이에서 발생하는 시퀀스와 현저히 유사한 특성을 보여줍니다.
.Journal of Statistical Mechanics에 발표 된이 연구는 Primes의 조직이 Quasicrystals에서 발견되는 원자 조직인 아페리오드 원자 조직을 가진 이상한 결정과 같은 재료와 현저한 유사성을 가지고 있음을 보여줍니다. 소수의 구성과 준결승의 조직은“Hyperuniform”으로 알려진 패턴의 종류에 속합니다. 이 지식의 잠재적 응용은 흥미 롭습니다. 수학자들은 숫자 선에서 소수의 위치를 예측할 수있는 알고리즘을 오랫동안 찾았지만 아직 그러한 알고리즘은 아직 발견되지 않았습니다.
연구원들에 따르면, 연구에서 얻은 지식은 숫자 라인에서 프라임을 예측하기위한 새로운 방법을 고안하는 데 도움이 될 수 있습니다. 이 연구의 수석 연구원 인 Salvatore Torquato는“이전에 발견 한 것보다 훨씬 더 많은 순서가있다”고 말했다.
소수, 준결음 및 과도한
소수는 유일한 요인이 하나이고 그 자체의 숫자입니다. 3, 7, 11 또는 2-1과 같은 숫자. 매우 큰 소수는 현대 암호화의 빌딩 블록입니다. 소수는 숫자 라인에 다소 무작위로 분포 된 것 같습니다. 현재 프라임을 생성하기위한 알고리즘은 없지만 수학자들은 조직에 대한 매우 일반적인 특징을 결정할 수있었습니다. 숫자 라인에서 더 많은 소수가 확산됩니다. 또한 무작위로 선택된 숫자가 소수 일 가능성은 해당 숫자의 숫자 수에 반비례합니다.
전문적으로 훈련 된 화학자 인 Torquato는 X- 선 결정학에 익숙합니다. X- 선 결정학에 익숙합니다. 다이아몬드 또는 석영과 같은 순서 및 주기적 결정의 경우, 결정학은 브래그 피크라고 알려진 밝은 반점의 예측 가능한 패턴을 초래합니다. 준결승은 일반 결정의 주기적 구조가 없기 때문에 규칙적인 결정과 비교하여 준 결정은 브래그 피크의 독특하고 복잡한 패턴을 나타낸다.
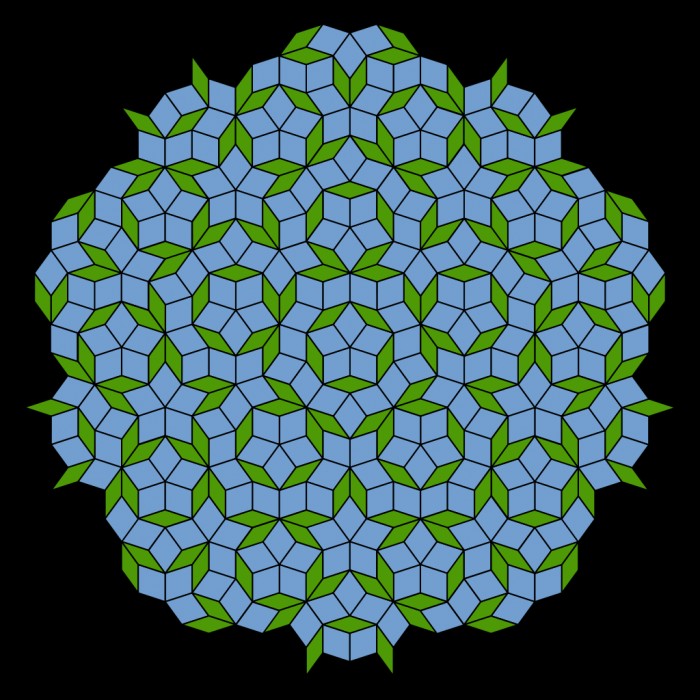
2 월에 발표 된 이전의 연구에서, 팀은 강력한 컴퓨터 시뮬레이션을 사용하여 소수가 X- 선에 따른 격자로 배열 된 원자처럼 처리되면 어떤 일이 발생하는지 보여주었습니다. 결과는 프라임 주문 된 결정이 준 결정의 것과 매우 유사한 브래그 피크 패턴과 "제한주기 순서"라는 다른 종류의 시스템을 보여 주었다. 현재 논문은 이전 실험의 수치 결과에 대한 이론적 설명을 제공하기위한 것입니다.
이러한 모든 조직은 "Hyperuniform"재료로 알려진 패턴의 클래스에 속합니다. 과잉 균일 한 재료 (때로는 "초 호색성"이라고도 함)는 명백한 순서가 없지만 대규모로 특수 조직 구조를 취하는 것으로 보입니다. 모순적으로 들릴지 모르지만, hyperuniform 자료가 "순서 혼란"중 하나라고 말할 수 있습니다. 조각은 작은 규모로 무작위로 배열 된 것처럼 보이지만 새의 눈에 광기에 대한 명령이 있습니다.
.2000 년대 초반에 과민성의 개념의 기원이 있기 때문에, 닭의 눈, 준결승 분포, 무작위 수의 분포, 입자의 양자 앙상블, 심지어 우주의 대규모 구조를 포함하여 자연에서 hyperuniform 조직 패턴이 발견되었습니다. Fibonacci 시퀀스와 마찬가지로, 과잉 균일 성의 수학적 패턴은 자연에서 발견되며, 그들의 예상치 못한 발견은 거의 항상 과학자들을 놀라게합니다.
이 경우 Torquato와 Cohorts가 소수로 발견 된 패턴은 정적 결정 및 기타 제한 기간 순서 시스템의 패턴과 유사하지만 이름을“효과적으로 제한 순서”라는 이름을 부여하기에 충분히 다릅니다. 프라임은 "자기 유사한"그룹으로 나타납니다. 이는 동일한 높이의 피크 사이에 더 작은 피크의 그룹이 있음을 의미합니다.
수학과 링크
이 모든 것이이 연구는 동일한 수학적 규칙이 숫자 라인의 프라임 분포와 특정 재료의 3 차원 원자 구조의 기본이라는 것을 시사한다. 한 도메인에서 개선 된 수학적 개념이 놀랍게도 다른 도메인에서 적용되는 것으로 밝혀진 경우가 종종 있습니다. 20 세기 초 물리학 자들은 그 당시 흥미로운 수학적 호기심이 일반 상대성 모델로 적용 될 수 있다는 사실을 알게되었을 때 분명히 놀라운 일이었습니다. 마찬가지로, 양자 역학의 초기 개척자들은 매트릭스 대수가 실제로 초기 양자 이론에 적용되었다는 것이 밝혀 졌을 때 놀랐습니다. 다시 한 번, 우리는 과도하게 균일 한 두 가지 영역에서 머리를 뒤로 두는 특정 수학적 개념을 봅니다 - 재료 과학과 숫자 이론.
Torquato와 그의 동료 분석 결과는 과학계에 흥미 롭습니다. 이 연구에 관여하지 않은 Microsoft의 연구원 인 Henry Cohn에 따르면,“이 논문에 대해 흥미로운 점은 프라임에 대한 다른 관점을 제공한다는 것입니다. 숫자로 보는 대신 입자로보고 X- 선 회절을 통해 구조를 매핑하려고 시도 할 수 있습니다.”
.새로운 정보가 소수를 생성하기 위해 알고리즘을 생성하는 데 길이가 길어질 수 있으며, 이는 우리가 알고있는 것처럼 수학의 전체면을 바꿀 수 있습니다.
.어떤면에서, 새로운 연구는 수학과 과학 사이의 관계에 대한 전통적인 이해를 다소 반전합니다. 일반적으로 과학자들은 수학을 사용하여 물리적 세계에 대한 예측을하지만 이제는 물리적 세계를 사용하여 수학에 대한 예측을 할 수있을 것 같습니다! 갈릴레오 갈릴리 (Galileo Galilei)는 종종 우주의 책이 수학 언어로 쓰여졌 고 그 캐릭터는 삼각형, 서클 및 기타 기하학적 인물이라고 말하는 것으로 인정됩니다. 이 교훈은 400 년 후에도 진실 된 것 같습니다.