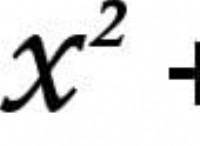발사체의 움직임은 중력의 영향을 받기 때문에 포물선입니다. 중력은 발사체가 직선이 아닌 곡선 경로에 떨어집니다. 발사체 운동의 방정식은 중력의 힘을 고려하여 발사체의 경로가 항상 포물선입니다.
대포에서 대포 촬영이 왜 수직으로 내려 가지 않고 오히려 곡선 적으로 쏘는가? 던져진 창 던지기가 땅을 찌르기 전에 호화로운 호를 그립니다. 발사체의 특성에 관계없이, 공기를 통해 아크는 정확하게 포물선입니다.
그 이유는 물론 중력이 예상 된 후 운동에 영향을 미치는 유일한 힘입니다. 그러나 우리가 본질적으로 요구하는 것은 왜 중력이 포물선을 추적하도록 강요합니까? Kepler는 행성들이 타원에서 태양을 공전했다는 것을 알고 있었지만 왜 을 몰랐습니다. 그들은 그렇게했다. 같은 맥락에서 왜 발사체는 다른 모양을 추적하지 않습니까?
방정식
물론, 이것은 발사체가 지구 표면에 수직으로 투영 될 때 사실이 아닙니다. 포물선 궤적을 관찰하려면 표면과 약간의 각도로 투사해야합니다. 수평력이 발사 후 발사체에 영향을 미치지 않더라도, 영광스러운 여정을 가능하게하는 것은 초기 수평력입니다. 수평 인력이 제공되지 않으면 창 던지기가 수평 거리를 어떻게 이동할 수 있습니까?
17 세기에 인류는 아직 로켓을 만들지 않았으며 가장 강력한 망원경은 토성보다 더 멀리 보일 수 없었습니다. 이러한 제약에도 불구하고, 영국의 작은 방에서 뉴턴이 어떻게 행성들이 태양을 공전하는 것이 아니라, 당시의 가장 저명한 철학자들이 원으로 믿었을 때 (또는 오히려 희망을 가진) 타원으로 어떻게 태양을 공전한다는 것을 발견 할 수 있었습니까? 물론 수학.
Newton은 지구와 태양 사이의 거리와 주위의 회전하는 동안에 걸친 각도 사이의 관계를 발견함으로써 Kepler의 주장을 증명했습니다. 그는 타원을 추적하는 포인트를 묘사하는 것이 정확히 같은 관계라는 것을 발견했습니다. 그러나 그의 평가는 그의 새로 제안 된 중력 법칙에 근거했다. 그의 법이 사실이 아니라면 그의 증거도 무너질 것입니다. 우리는 이제 그가 제안한 것이 사실이라는 것을 알고 있습니다. 뉴턴은 중력 가 무엇인지 설명하지 않았다 그러나 그는 그것이 어떻게 작동하는지 아름답게 설명했다.
마찬가지로, 발사체 흔적을 곡선으로 결정하기 위해서는 동작과 그에 해당하는 곡선을 설명하는 방정식을 찾아야합니다.
.
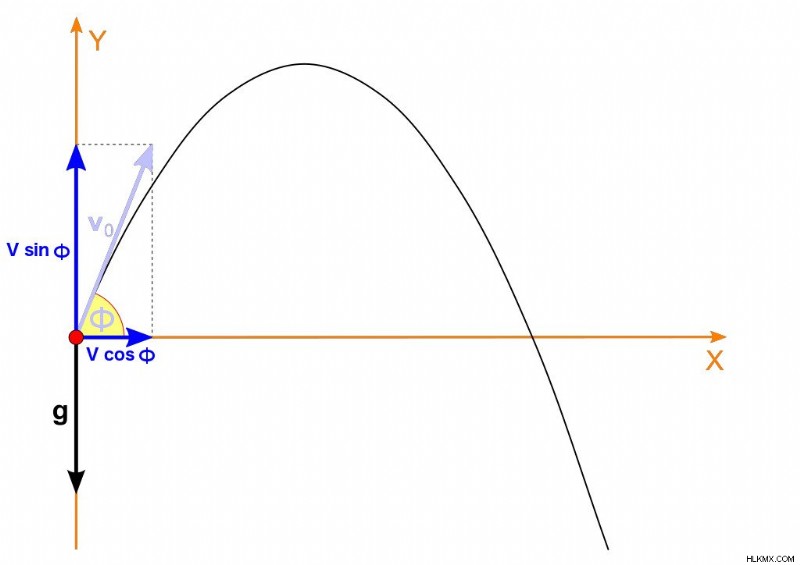
(사진 크레딧 :Sándor Zátonyi / Wikimedia Commons)
발사체는 표면과 관련하여 초기 속도 'v'가 각도 'φ'로 투영됩니다. 발사체가 수평으로 이동하는 거리는 (x 축에서) x =vtcosφ 로 제공됩니다. (v =x/t). 그러나 수직으로 이동하는 거리 (Y 축에서)는 y =vtsinφ-(½) gt² 로 주어집니다. . 이것은 수직으로 발사체가 힘을 경험하고 가속화, 즉 중력으로 인한 가속도, 'g'로 표시되기 때문입니다.
.이제이 가속도가 일정하기 때문에 운동 학적 방정식 s =ut + (½) at² 을 사용할 수 있습니다. ‘Y’거리를 계산합니다. 여기에서‘U’는 초기 속도이며,이 경우 vsinφ 입니다. ‘A’는 끊임없는 가속도이며,이 경우 선택된 협약으로 인해‘-g’입니다. 따라서 수직 거리 y =vtsinφ - (½) gt² .
‘X’측면에서‘Y’를 찾거나‘Y’와‘X’의 관계를 설명하는 방정식을 얻으려면 첫 번째 방정식에서‘T’를 해결하고‘Y’에서 그 값을 대체합니다.
.
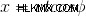
또는, 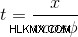
t in의 값을 대체하십시오. 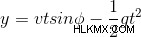
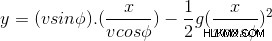

여기, tanφ 및 g/2v²cos²φ 상수이므로 방정식은 방정식 y =ax+bx² - 과 비슷하게 비슷합니다. 포물선의 방정식!