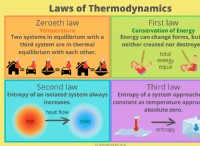
가장 간단한 유형의 가속 운동은 직선과 일정한 가속으로 움직임입니다. 속도는 움직임이 진행되는 것과 동일한 속도로 변합니다. 일정한 가속으로 직선으로 움직임을 다루는 대부분의 숙제 문제를 해결할 수있는 세 가지 기본 운동 방정식이 있습니다.
(1) x =x 0 + v 0 t + ½at
(2) v =v 0 + at
(3) v =v 0 + 2a (x - x 0 )
어디
X는 이동 거리입니다
x 0 초기 시작점입니다
V는 속도입니다
v 0 초기 속도입니다
A는 가속입니다
t는 시간입니다
이 작업이 일정한 가속도 예제 문제는이 세 가지 운동 방정식을 사용하여 파괴 차량의 위치, 속도 및 가속도에 대한 세부 사항을 찾는 방법을 보여줍니다.
.
예제 문제 :
운전자는 120km/hr로 속도를 높이고 있습니다. 그는 멈추려 고하지만 차가 멈추는 데 12 초가 걸립니다.
(a) 자동차의 가속은 무엇입니까? (가속도가 일정하다고 가정)
(b) 다람쥐가 살아남는가?
(c) 자동차가 100 미터로 얼마나 빨리 움직였습니까?
솔루션 :
이것은 처음에 차량의 조건 (t =0 초)을 보여주고 자동차가 정지되었을 때 (v =0 km/hr)
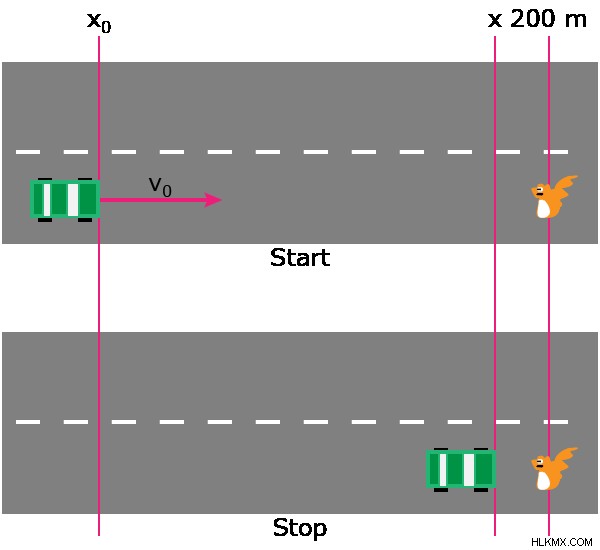
파트 a) 가속도를 찾으십시오.
위에서 방정식 2를 사용하십시오.
v =v 0 + at
t =12 초와 v 0 를 사용하십시오 =120km/hr. 첫째, 정지 시간이 몇 초에 표시되지만 속도는 시간당입니다. 우리는 또한 미터에있는 거리가 필요하므로 속도를 m/s :
로 변환하십시오.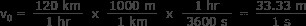
v 0 =33.33 m/s
차가 끝에서 멈추므로 최종 속도는 0입니다.
0 =33.33 m/s + a (12 초)
-33.33 m/s =A (12 초)
a =-2.78 m/s
가속도는 음수입니다. 이것은 움직임이 긍정적 인 방향으로 진행됨에 따라 차량을 늦추고 있음을 의미합니다. 차량의 속도가 느려지는 문제에서 기대할 수있는 것.
Part B) 다람쥐가 살아남습니까?
다람쥐가 살아남은지 알아 내려면 차량이 멈추기 전에 얼마나 멀리 여행했는지 알아야합니다. 이동하는 거리는 다람쥐까지의 거리보다 작 으면 다람쥐가 살아남을 것입니다. 이 부분에 대해 위에서 방정식 1을 사용하십시오.
x =x 0 + v 0 t + ½at
파트 a)와 초기 조건에서 가속도를 연결하십시오.
x =0 m + (33.33 m/s) (12 s) + ½ (-2.78 m/s) (12 초)
x =399.96 m - 200.16 m
x =199.8 m
차량이 멈추는 거리는 200m 미만 이었으므로 다람쥐는 만남에서 살아 남았습니다.
파트 C) 100 미터의 속도는 얼마입니까?
이 부분에 대해 위에서 3 방정식을 사용하십시오.
v =v 0 + 2a (x - x 0 )
x =100 미터와 m/s의 속도 단위와 m/s의 가속도를 사용하십시오.
v =(33.33 m/s) + 2 (-2.78 m/s) (100 m-0m)
V =1110.89 m/s - 556 m/s
v =554.89 m/s
V =23.56 m/s
차량은 100 미터 마크에서 23.56m/s (84.8km/hr)에서 움직이고있었습니다.