우리의 마지막 통찰력 퍼즐은 Galton 보드 또는 Bean 머신이라는 고전적인 결정 론적 기계에서 부드럽고 무작위로 분포하는 방법을 탐구했습니다. 우리는 퍼즐을 가지고 놀면서 이것의 내부 작업을 조사했습니다. 나는 또한 Galton Board의 확률 적 결과를 사용하여 아마도 양자 역학의 확률 론적 방정식이 우리가 특권을 얻지 못한 기본 결정 론적 법률에서 튀어 나왔다고 제안했습니다. 독자들은 퍼즐 질문과 철학적 제안에 모두 반응했다. 퍼즐 질문을 먼저 살펴 보겠습니다.
아래에서 볼 수 있듯이 Galton 보드는 대리석이 위에서 아래로 굴릴 수있는 여러 경로를 생성하는 페그 행이있는 직립 보드로 구성됩니다. 대리석은 상단에 떨어지고 페그가 발생할 때 동일한 확률로 오른쪽 또는 왼쪽 경로를 취합니다. 바닥에서 구슬은 한 번의 쓰레기통에 쌓여 파스칼의 삼각형과 가우스 분포를 재현 할 수 있습니다.
퍼즐 1 :빈은 평등을 요구합니다!
위 그림에 표시된 종류의 Galton 보드가 있다고 상상해보십시오. 이것은 여덟 번째 줄 대신에 쓰레기통이 있으며 전통적인 동등한 확률 페그가 있습니다. 바닥에있는 각 빈이 같은 수의 대리석을 모으도록 수정하려고합니다. 당신은 당신이 전통적인 못 중 일부를 대리석을 왼쪽이나 오른쪽으로 불평등하게 지시하는 새로운 못으로 교체해야한다는 것을 알고 있습니다. 대리석을 전적으로 왼쪽으로, 전적으로 오른쪽으로 또는이 두 극단 사이의 비율로 지시하는 페그를 선택할 수 있습니다.
.모든 쓰레기통에 대한 완전한 평등의 목표를 달성하기 위해 교체해야 할 가장 적은 수의 페그 수는 얼마이며, 왼쪽 비율은 얼마입니까?
보너스 질문으로 위의 결과를 모든 크기의 Galton 보드에 일반화하는 공식을 도출하고 정당화 할 수 있습니까?
Rob Corlett 은이 문제에 올바르게 대답했으며 Thana Somsirivattana는 공식적인 증거를 제출했습니다. 28 개 중 10 개의 페그 만 교체해야한다는 것이 밝혀졌습니다. 교체 페그는 간단합니다. 단순히 왼쪽 (L 페그) 또는 오른쪽 (r 페그)에 부딪 치는 대리석을 라우팅합니다. Lionel Lincoln과 Rob Corlett의 협약에 따라, 우리는 평등 확률 PEGS 표준 페그를 호출 할 수 있습니다. 다음은 페그가 어떻게 배열되는지와 128 개의 구슬을 노선하는 방법을 보여주는 해결책입니다.
배열은 멋지고 규칙적이며 교체 못이 왼쪽과 오른쪽으로 내려갑니다.
보너스 질문의 경우,이 배열은 빈의 수가 2의 힘 인 다른 경우에 일반화됩니다. 다음 공식은 Rob Corlett에 의해 재귀 적으로 도출되었습니다. 여기, p ( n ) n 가있는 보드의 비표준 페그 수입니다. 쓰레기통 :
p (1) =0
p (2) =0
p ( n ) =2 p ( n /2) + n - 2
따라서 4- 빈 보드에 필요한 교체 수는 2 p 입니다. (2) + 4-2 =2 × 0 + 2 =2. 16 쌍 설정의 숫자는 2 × 10 + 16-2 =34입니다.
빈의 수가 2의 전력이 아닌 경우 문제가 훨씬 어려워집니다. Rob Corlett의 말에 따르면,“이것은 구조를 파헤칠 때 엄청나게 복잡한 문제입니다!” 대수적 접근법을 사용하여 Corlett은 2 개의 솔루션에서 일반화하고 AN n 에 대한 최소 대체에 대한 상한을 나타내는 다음 공식을 도출했습니다. -Bin 보드 여기서 n 2 :
의 힘이 아닙니다p ( n ) = p ( m ) + p ( n - m ) + n - 1
여기서 m n 보다 작은 2 개의 가장 큰 힘입니다 .
Cornflower가 다양한 크기의 보드에 선형 프로그래밍을 사용하여 보여 주었기 때문에 이것보다 더 잘할 수 있다는 것이 밝혀졌습니다. Cornflower는 Galton 보드에 대한 최소 솔루션의 예를 제공합니다. 5 층 보드의 경우 교체 해야하는 최소 페그 수는 5 개, 6 쌍 보드의 경우 6 개, 7 번 보드의 경우 8 개입니다.
숫자는 위의 경우 원래 페그를 행의 끝에 남겨 둘 수 있기 때문에 공식에 의해 예측 된 것보다 작습니다. 이러한 모든 경우에 Rob Corlett이 대수적으로 보여 주듯이 몇 가지 최소 교체 구성이 가능합니다. Cornflower는 또한 Corlett이 독특한 것으로 보이는 12-bin 설정에 대칭 솔루션을 제공했습니다.
이 두 기고자로부터 위대한 작품을 읽는 것이 좋습니다. kudos!
퍼즐 2 :트윈 피크
퍼즐 1에서와 같이 전통적인 Galton 보드로 시작하지만 이번에는 바닥에 9 개의 쓰레기통이 있습니다. 하단의 구슬 분포가 다음과 같습니다. 0, x , 2 x , x , 0, x , 2 x , x , 0, 여기서 x 총 대리석 수의 1/8을 나타냅니다.
Rob Corlett은 다음과 같은 우아한 솔루션을 제공하며, 이번에는 8 개의 교체 페그가 대칭 적으로 배열되어 있습니다.
퍼즐 3 :개별 행동 예측
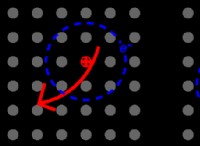
이 그림에서, 대리석은 4 열의 4 개의 위치 중 하나에있는 경우 0의 "드리프트"를 가졌으며 화살표에 의해 표시된대로 8 행의 해당 위치에있게 된 경우. 다른 통에서 끝나면 드리프트의 값은 예상 빈으로부터의 거리의 제곱과 같습니다. 따라서, 대리석이 4 열에서 가장 왼쪽 위치에서 시작하여 7으로 표시된 쓰레기통에서 끝났다면, 예상 쓰레기통의 왼쪽에있는 1 개의 빈은 1 =1입니다. 드리프트는 1 =1입니다. 드리프트가 최종 행에서 가장 왼쪽 쓰레기통에서 끝나면 (표시된 1), 드리프트는 2 =4입니다. 특정 Galton 보드의 평균 드리프트는 8에서 4로 움직일 때 마블의 평균 드리프트입니다.
평균 드리프트는 무엇입니까 :
1. 원래 Galton 보드.
2. 퍼즐에서 수정 된 Galton 보드 1
3. Puzzle 2에서 수정 된 Galton 보드.
Rob Corlett은 답변을 다시 한 번 정확하게 제시했습니다. 그들은 1, 1.5 및 2.5입니다. Corlett은 문제를 단순화하는 영리한 팁을 제공합니다.“여기서 트릭은 Row 4에 떨어지는 공의 공이 1 행에서 들어오고 5 행에 떨어지는 것과 효과적으로 동일하다는 것을 알 수 있습니다.”
.이제 많은 흥미로운 독자 의견을 도출 한 철학적 질문에 대해 논의 해 봅시다. 이 중 일부를 논의하기 전에 내가 어디에서 왔는지에 대해 두 가지 점을 만들고 싶습니다.
첫째, 내 관점은 주어진 양자 사건에 대한 인과 사슬에만 관심이있는 과학자의 관점입니다 (예 :이중 슬릿 실험의 맨 끝에서 특정 지점을 때리는 광자). 나는 확률 론적 공식이 있다는 것을 알고 있지만, 존 벨이 "비 블리즈 (Beables)"라고 부르는 것에 대답하지는 않습니다. 일부 선행자는 광자를 그 특정 지점으로 추진했을 것입니다. 다른 점은 광자, 환경, 환경, 실험이 수행 될 것이라는 실험의 특정 부분에서 우주의 복잡한 상호 작용과 같은 것이어야합니다.“이 팀의 관점에서 볼 때, Photon은 무작위로 지정하고있다”고 말했다. 본질적으로 확률 론적입니다. 분명히 임의의 선택은 전례없이 제로 시간에 이루어지지 않았습니다. 광자의 선택에 앞서 Yoctosecond의 작은 부분을 검사 할 수 있다면, 그 선택이 일어난 일이 일어났습니다.
.그래서 이것은 나의 두 번째 요점입니다. 나는 어떤 우주에서도 선구자가없는 순수한 임의의 선택이 어떻게 논리적으로 가능한지 알지 못합니다. 양자 무작위성은 완벽하고 내재 된 것처럼 보일 수 있습니다. 왜냐하면 우리가 관찰하기를 희망하기에는 너무 작은 수준의 선구자에 의해 발생하기 때문입니다. 그러나 선행자들은 존재해야합니다. 주사위의 무작위성과 다른 모든 무작위 현상과 같은 무작위성은 우리의 무지에 의해 발생합니다. 나는 다른 독자의 의견에 대답 한 Segrimm에 동의합니다.“죄송합니다. 우리의 우주가 비 지역적으로 행동하기 때문에 단일 이벤트도 결정됩니다. 결정은 현지 현상의 '내부 및 외부'의 모든 변화의 결과입니다. 우리가 결과를 예측할 수 없다는 사실이 결과가 결정되지 않았다는 것을 의미하지는 않습니다.”
그건 그렇고, 몇몇 독자들은 왜 내가 두 적대적 관점 팀 E (Albert Einstein)와 Team B (Niels Bohr)를 지명 한 이유에 의문을 제기했습니다. 나는 Solvay Conference에서 일어난 토론을 암시하고 1927 년 양자 역학이 탄생 직후 세계 최고의 물리학 자들을 모았습니다. 두 가지 반대되는 견해의 지도자들은 아인슈타인과 보어였으며, 그는 격렬하게 논쟁을 벌이고 서로 잠 못 이루는 밤을주는 포인트와 반점을 높였습니다. 마지막으로, 보르의 고유 한 무작위성에 대한 관점은 떠오르는 코펜하겐 해석의 일부로 우세했으며, 아인슈타인의 견해는 그의 유명한 느낌표에 캡슐화되었습니다.“하나님은 우주와 주사위를하지 않습니다.” Bohr의 팀의 저명한 물리학 자들은 Werner Heisenberg, Paul Dirac, Wolfgang Pauli 등 대부분의 다른 사람들이었습니다. 아인슈타인의 팀에는 De Broglie가 있었고 나중에 Bohm과 Bell이있었습니다. 유명한 방정식이 공식 팀 B 조회수에 기여한 Erwin Schrödinger는 나중에 클래식 Schrödinger의 고양이 사고 실험을 제안함으로써 팀 E를 위해 결함과 강제로 주장했습니다.
이제 철학적 반응 중 일부를 살펴 보겠습니다.
TJ_3rd는“MWI (Mony Worlds 해석)가“작은 입자가 사소한 입자가 사소한 선택을 할 때마다 수많은 우주가 복제되고 있다고 가정합니다. 물론, 그것은 좋을 것입니다. 그리고 링크에 감사드립니다! 그러나 위의 선언 된 관점을 감안할 때, 이것이이 토론에 어떤 영향을 미치는지 알 수 없습니다. TJ_3rd가 말하면서“에버렛은 그의 '많은 세계 해석'이 어떻게 개인의 결과를 예측하지 못하고 예측할 수 없는지에 대해 자세히 설명했습니다. " 그러나 개별 결과의 원인은 내가 궁금한 것입니다. MWI가 우주의“복제”와“선택”을하는 입자를 제안한다는 나의 믿음에 관해서는, 이것들은 나의 말이 아니라, 다중 평행의 우주가 존재하거나 실제로 존재한다고 믿는 David Deutsch와 같은 에버렛의 일부를 추종하는 사람들이 사용하는 사람들. 나는 이것을 구독하지 않는 다른 추종자들이 있다는 것을 알고 있습니다. 분명히 MWI의 "다른"세계는 실제 또는 비현실적인 두 가지 해석을 가질 수 있습니다. 그러나 세상이 비현실적이라면, 에버렛 절차는 단지 수학적 인공물 일 뿐이며, 슈뢰딩거 방정식에 흩어져있는 양자 진화가 존재하는 유일한 과정이라고 상상할 수있는 수학적 인공물 일뿐입니다. 그러나 이것은 Schrödinger 방정식이 진정한 운동 방정식 인 경우에만 의미가 있습니다. 그렇지 않습니다. 가우스 분포가 Galton 보드의 결과를 확률 적으로 표현하는 것처럼 확률 론적 표현입니다. 따라서 위에서 언급 한 마법의 고유 불확실성을 배제한다면 앙상블을 참조해야합니다.
.존 리치 필드 (Jon Richfield)는 결정론과 인과 관계 사이에 차이가 있으며 결정론은 무한한 측정의 정밀도를 필요로한다는 사실을 지적합니다. 혼돈 이론에서 알 수 있듯이, 완전히 결정 론적 인 세상을 옹호 한 피에르-시몬 라플라스 (Pierre-Simon Laplace)는 고전적인 의미에서도 틀렸지 만 예측 적으로 틀렸지 만 회고 적으로 잘못된 것은 아니었다. 복잡하지 않은 대부분의 고전적인 결과를 감안할 때, 초기 조건이 무엇인지 유한 한 정밀도와 그 결과로 이어진 경로로 유한 한 정밀도로 추론 할 수 있습니다. 당신이 할 수 없다면, 당신의 법률은 불완전합니다. 그러나 나는 현재의 주장에 대해 인과 관계에있는 것처럼 엄격한 결정론에별로 관심이 없다는 데 동의한다.
Zden commentk Skoupý는“우리가 공의 움직임의 '인과성'을 훨씬 더 세부적으로 해결한다면 원칙적으로 우리는 무한대로 갈 수 없다. 끝은 양자 수준에있다”고 말했다. 그러나 볼은 우리가 행동을 결정하기 위해 양자 수준으로 이동할 필요가없는 거시적 대상에 충분히 큽니다. 실용적이고 실제적인 Galton 보드에서 공이 어떤 방식으로 진행되는지 결정하는 무작위 물리적 메커니즘은 고전적으로 완전히 설명 될 수 있다고 생각합니다. 거시적 대상으로서의 움직임은 양자 세계에서 효과적으로 봉인됩니다.
.Galton 보드와 같은 것이 더블 슬릿 결과를 제공하기 위해 작동한다는 Devin Wesley Harper의 아이디어는 흥미 롭습니다. 그러나, 이중 슬릿 패턴은 각각의 광자가 그 자체를 방해함으로써 발생하는 간섭 패턴이라는 확신이 있음을 명심해야한다는 점을 명심해야한다. 또한 패턴은 진공 상태에서도 발생합니다. Devin, 당신의 이론은 성공적이라면이 두 가지 경고를 설명해야합니다. 어떻게 진행되는지 알려주세요.
그게 지금은 모든 것입니다. 의견을 말한 모든 분들께 감사드립니다. 이 토론을 계속하려면 여기에 의견 섹션에서 그렇게 할 수 있습니다. 나는 분명히 박수를 보내려고 반응하려고 노력할 것이다.
이번 달의 통찰력 상은 Rob Corlett에게 간다. Cornflower에 대한 명예로운 언급은 다음과 같습니다. 귀하의 기여에 다시 한번 감사드립니다. 축하합니다!