제 4 차원에 대한 올 인 클루 시브 여행 패키지에 관심을 가져 주셔서 감사합니다. 다음은 예비 탐험가로부터 가장 자주 묻는 질문입니다. 지금까지 우리의 고객 중 어느 누구도 돌아 오거나 텍스트를 보냈으므로 과학 컨설턴트가 말한 내용 만 공유 할 수 있습니다.
어떻게 거기에 도착합니까?
당신은 큰 구의 중심에 서 있습니다. 현재의 3 차원 현실에서 나올 것으로 예상 할 수 있듯이 왼쪽 또는 오른쪽, 앞으로 또는 후면 및 위 또는 아래로 이동할 수 있습니다. 그러나 특허받은 4-D Boost® 기술을 한 번에 구 표면의 모든 지점에서 벗어나 네 번째 차원으로 들어 올리는 동안 가능한 한 가능한 한 유지하도록 요청합니다.
.허? 내 사무실의 기술 지원 담당자는 여행에 큐브가 포함될 것이라고 말했다.
큐브는 4 차원 공간을 이해하는 데 유용한 도구입니다. 예를 들어 (1-D) 라인 세그먼트부터 시작하겠습니다. 평행 세그먼트를 추가하고이를 수직 세그먼트 2 개, 모두 똑같이 크기로 연결함으로써 (2 차원) 사각형을 만들 수 있습니다. 지금까지 우리와 함께? 마찬가지로, 우리가 두 개의 평행 사각형을 가져 와서 더 많은 수직 세그먼트와 연결하면 (3-D) 큐브를 얻습니다. 이제 상황이 까다로워지는 곳이 있습니다. 다음 반복에서 2 개의 병렬 큐브와 수직 커넥터가 (4-D) 하이퍼 큐브 또는 TesserAct를 만듭니다.
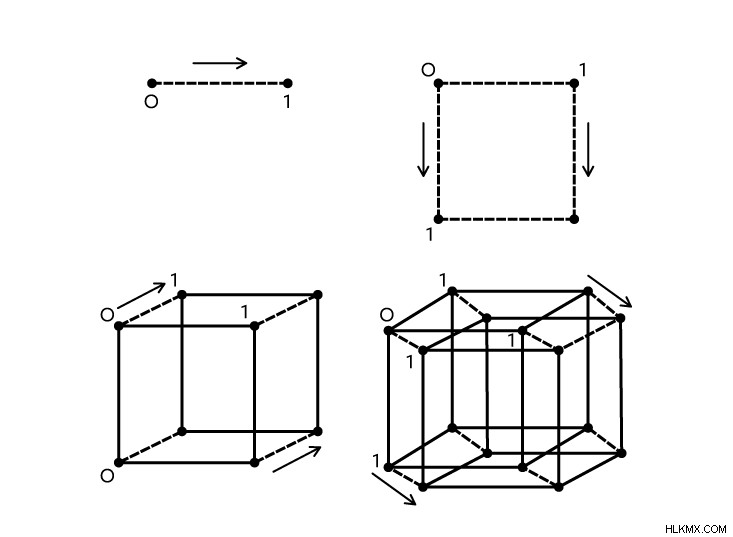
물론, 3D 생물이기 때문에 우리는이 4D 구조에 대한 우리의 마음을 완전히 감쌀 수 없습니다. 후기 수학자 윌리엄 서 스턴 (William Thurston)은 이것이 우리의 두뇌가 한 영역에서 선형 분석 정보와 다른 영역에서 형상을 처리하기 위해 진화했기 때문이라고 믿었습니다. 따라서 우리는 4 개 이상의 변수로 방정식을 쉽게 해결할 수있어 더 높은 차원에서 객체를 꿈꾸고 조작 할 수 있지만, 우리는이를 인식하기 위해 고군분투합니다. 호주 수학자 (및 스탠드 업 코미디언) Matt Parker는“네 번째 차원은 우리가 가진 세 가지 차원에 직각으로 생각할 수 있습니다. . “그러나 우리는 4 차원이 무엇인지 상상할 수 없습니다 .”
그래서 당신은 내가 거기에 도착하기 전에 내 호텔의 사진을 볼 수 없다고 말합니까?
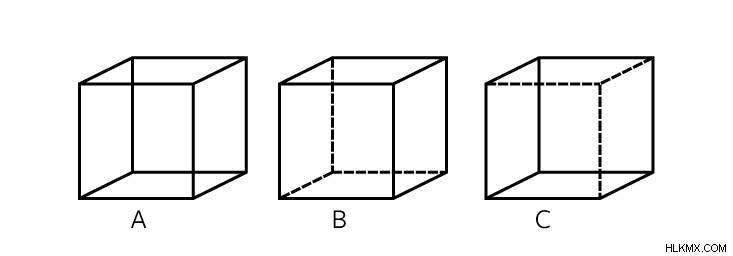
불행히도, 아니요. 그러나 Necker Cube (아래 그림에 레이블이 붙은)라는 착시를 통해 네 번째 차원을 엿볼 수 있습니다. 이 모양을 해석하는 두 가지 방법이 있습니다 :상자는 약간 왼쪽과 아래로 (b) 또는 거울 이미지 (c)로 지향합니다. 네커 큐브를 충분히 쳐다 보면 수학자 루디 루커 (Rudy Rucker)가 "반짝 반짝 반복"이라고 부르는 것과 앞뒤로 뒤집는 것처럼 보입니다. 결국 반짝이는 것은 하나의 연속적인 움직임으로 보일 수 있습니다. 그러나 Rucker가 그의 책 기하학, 상대성 및 4 차원에서 지적한 것처럼 , "이 움직임은 4D 공간에서 회전하는 경우에만 연속적 일 수 있습니다." 3 차원의 회전은 거울 이미지를 생성 할 수 없기 때문입니다. "아마도 우리는 실제로 우리의 마음에 4D 현상을 생산할 수 있습니다!"
흠… 아마도 이것은 나를위한 것이 아닐 수도 있습니다.
역학에 너무 매달리지 마십시오. 롤러 코스터가 라이딩을 즐기기 위해 어떻게 작동하는지 알 필요가 없습니다.
좋아, 그래서 나는 무엇을 포장해야합니까?
우리는 다음을 포함하여 필요한 모든 것을 제공 할 것입니다.
열 차폐. 여분의 차원은 안정적인 궤도에서 지구를 회전시키는 중력과 원심력 사이의 섬세한 균형을 방해합니다. 후기 물리학 자 Richard Morris에 따르면, 일단 4D 공간에 도착하면 지구는 태양을 향해 나선 다.
편광 렌즈. 빛은 전기 및 자기장에 수직 방향으로 전파되기 때문에 다른 수직 좌표 세트를 추가 할 때 어떻게 행동 할 것인지 예측하기가 어렵습니다. 따라서 선글라스는 아프지 않습니다. Rucker에 따르면 디스크가 아닌 구 모양, 즉 "제 3의 눈"도 유용 할 것입니다. 그러나 소송이 진행 중이기 때문에 더 이상 수술을 제공하지 않습니다.
이어 플러그 . 연못의 잔물결처럼 치수의 소리가 더 두 배로되므로 모든 것이 반향을 일으키고 끌어 당기고 소음으로 끊임없이 폭격 할 수 있습니다. 예를 들어, 베토벤의 다섯 번째 교향곡 (Dum dum dum dah)의 시작은“mushed out”이 될 것입니다. , Hyperspace를 통한 서핑의 저자 인 Clifford Pickover는 말합니다 . 동료 여행자가 당신에게 말할 때 이해할 수 없다면 놀라지 마십시오.
벨크로 신발. 한쪽 끝이 3 차원으로 들어 올리면 비행기에 누워있는 루프 끈 조각이 곧게 나오는 것처럼, 3D 매듭은 4D 공간에서 쉽게 풀릴 것입니다. 우리는 당신이 거기에 도착할 때 당신이 당신의 끈으로 (한 번에 여러 방향으로) 여행하는 것을 원하지 않습니다.
닫힌 끈의 루프, 두 개의 나무 고리 및 조개. 독일 천체 물리학 자 Johann Zöllner가 1878 년에 조언 한 것처럼,이 항목을 사용하여 실제로 네 번째 차원에 도달했음을 확인합니다. 루프를 자르지 않고 끈에 매듭을 묶고 고리를 링크하고 링크하고 해안의 나선 방향을 뒤집을 수 있어야합니다.
나는 4D 생물에 의해 공격을 받거나 습격 될 것인가?
우리는이 가능성을 배제 할 수 없습니다 (면제 참조). 그들의 두뇌에 훨씬 더 많은 신경 연결이 있으면 4D 존재는 매우 똑똑 할 것입니다. 그리고 Parker가 우리에게 알리면, 그들은“궁극적 인 전술적 이점을 가질 것”입니다. 유사하게, 3D 생물 인 당신이 2D 생물을 괴롭히기를 원한다고 가정 해 봅시다. 피해자는 평평한 표면으로 제한되며, 눈에 띄지 않는 곳에 올라갈 수 있습니다. 모든 내부를보고 액세스 할 수 있습니다. 당신이 그것을 잡기 위해 세상에 손에 닿았다면, 손가락은 갑자기 떠 다니고 분리 된 원으로 나타납니다. 마찬가지로, 4D 공격자는 3D 시야에서 파란색에서 구체화되어 지갑에서 돈을 뽑거나 옷이나 피부에 손가락을 얹지 않고 장기를 수확 할 수 있습니다.

4D 생물은 영어를 할 것인가?
말하기 어렵습니다. Pickover의 조언에 따라 이진 코드로 통신하는 것이 좋습니다. (수학 규칙은 어느 차원에 사는 지에 관계없이 모든 차원에 적용됩니다.) 예를 들어, 당신은 깜박임을 시도하거나 팔을 위아래로 올릴 수 있으며 누군가가 알아 채기를 바랍니다. 4D 생물도 마찬가지로 플랫 평면에서 3D 물체를 삽입하고 제거하여 2D와 통신 할 수 있듯이 3D보기에서 4D 객체를 삽입하고 제거하여 메시지를 보낼 수 있습니다.
.물은 마시기에 안전합니까?
물이 전혀 존재한다면 괜찮을 것입니다. 이것에 대한 불확실성이 있습니다. 일부 물리학 자들은 수소 원자 (h in h 2 이라고 주장했다. o) Quantum Forces가있는 여분의 치수 나사는 중력을 망쳐 놓기 때문에 4 차원에서는 안정적이지 않습니다. 그러나 수학자 팀은 더 높은 차원이 일반적인 전자기 법칙을 따르지 않는다고 가정하면 결국 안정적인 수소 원자를 가질 수 있음을 발견했습니다. 안전하게 플레이하려면 출발 전에 많은 액체를 마시는 것이 좋습니다.
어떤 기념품을 사야합니까?
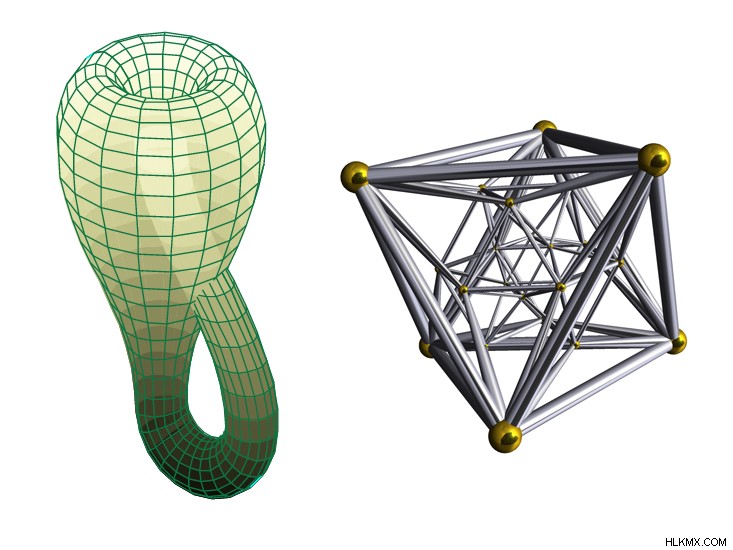
선물 가게에 Rubik의 하이퍼 큐브가 있는지 확인하십시오. ™ 캘리포니아의 일부 영리한 소프트웨어 엔지니어가 제작 한이 퍼즐의 온라인 버전을 이미 시도했을 수도 있지만, 이것은 4D 큐브의 3D 투영에 대한 2 차원 투영 일뿐입니다. 진짜는 훨씬 더 굉장 할 것입니다. Parker는 또한 좋아하는 4D 모양의 키 체인을 권장합니다. 하이퍼 큐브는 하이퍼 디아몬드 (또는 Octacube)로 알려져 있습니다. 플라톤 고체의 6 가지 4D 아날로그 중 하나입니다 (큐브 또는 사면체와 같은 면적이면)는 3D에 해당하지 않습니다. 또 다른 재미있는 기념비는 클라인 병으로 한쪽 ( "내부"및 "외부"없음)이 있고 경계가 없으므로 자체가 포함되어 있습니다. 구멍을 만들지 않고 스스로를 통과해야하기 때문에 4 차원으로 만 존재할 수 있습니다.
그러나 돈을 절약하고 싶을 수도 있습니다. 우리는 4D 공급 업체가 3D 관광객을 guge합니다. 게다가, 집으로 가져 오는 물건은 3D 공간에서 거의 인상적이지 않습니다.
만족하지 않으면 어떨까요?
가능한 모든 결과를 예측할 수 없으므로 환불을 제공 할 수는 없습니다. 그러나 신체가 거울 이미지로 회전하거나 8 방향으로 분리 된 경우, 3D 공간으로 돌아 오는 DNA 인증 기관과 같이이 일이 발생했다는 증거가 있다면 생존자들은 선물 가게에 50 달러의 바우처를 발행 할 것입니다.
.
chip Rowe는 뉴욕에 본사를 둔 작가입니다.
참조
1. Gardner, M. 거대한 수학 책 W.W. Norton &Co., New York, NY (2001).
2. Parker, M. Farrar, Straus and Giroux, New York, NY (2014).
3. Rucker, R. 네 번째 차원 :더 높은 현실의 기하학을 향해 Houghton Mifflin Co., Boston, MA (1984).
4. Morris, R. Wiley, New York, NY (1993).
5. Pickover, C. Hyperspace를 통한 서핑 :6 가지 쉬운 교훈에서 고등 유니버스 이해 옥스포드 대학 출판부, 뉴욕, 뉴욕 (1999).
6. Burgbacher, F., Lammersahl, C., &Macias, A. 더 높은 치수의 안정적인 수소 원자가 있습니까? 수학 물리학 저널 40 , 625-634 (1999).