Pascal의 법칙은“정적 유체의 한 지점에서 압력의 압력 또는 전력은 모든 경로에 해당한다”고 설명합니다. 용기의 흐르는 유체에 압력이 가해지는 경우, 용기 내부에서 압력이 동일하게 전달된다는 것을 나타냅니다.
.Pascal의 법칙은 결속 된 유체에 압력이 가해지면 어느 곳 으로든 흐르지 않을 때, 유체는 그 시점에서 유사한 속도로 모든 경로에 동등한 압력을 전송 (또는 전달)합니다.
.파스칼의 법에 대한 설명
1653 년 프랑스 수학자 Blaise Pascal에 의해 주어진 Pascal의 법칙에 따르면, 제한된 유체 또는 외부 압력이 적용될 때 균일 한 유체에서는 모든 방향으로 균일하게 전송 될 것이라고 명시하고 있습니다. 압력은 일정하게 유지되며 인클로저에 고르게 분포되어 인클로저의 벽에 직각으로 작용합니다. 여기에 적용된 압력이 일정하기 때문에
힘 =압력 X 영역
따라서 표면적이 증가함에 따라 압력이 일정하게 유지되는 동안 힘도 증가합니다. Pascal은 또한 유체의 시점에서 그것을 통과하는 모든 비행기에서 압력이 일정하다는 것을 발견했습니다. Pascal의 법칙은 많은 일상 제품에 사용됩니다. Pascal의 법칙은 자동차 산업에서 사용하는 유압 펌프 제작에 사용됩니다. 또한 올리브 오일 및 헤이즐넛 오일과 같은 프레스 오일, 압력 게이지 교정 및 Jackhammer 's, Paint Sprayers 및 트럭 브레이크에도 널리 적용됩니다.
실린더 내부의 피스톤은 모든 챔버의 분배기에 대항하여 액체가 챔버 밖으로 누출되지 않도록하고 공기가 챔버로 들어가는 것을 제한합니다. 주요 챔버의 피스톤이 힘을 적용 할 때마다 프레임 워크의 어느 곳에서나 압력이 증가합니다. 힘은 연관 실린더를 통해 후속 챔버와 도움이됩니다.
Pascal은 액체에 가해지는 힘이 압력 또는 액체를 통한 힘의 전달을 형성하는지 확인했습니다. 이 검사는 액체가 특성화되고 압력을받을 때 액체의 두 가지 주요 부분을 발견했습니다. 그것에 적용되는 압력은 모든 방식으로 유사하게 전달 되며이 압력은 컨테이너의 각각에 동등한 힘으로 작용합니다.
파스칼 법의 공식
다음은 Pascal의 법칙에 대한 공식입니다.
let, f 적용된 힘
p 전달 된 압력
a는 단면적이어야합니다
f =pa
파스칼 법의 예
예를 들어 파스칼 법칙의 작동 원리를 이해해 봅시다.
5000 Pa의 압력은 피스톤에 힘이 가해져 액체 컬럼 전체에 전달됩니다. 피스톤의 면적이 0.01m2 인 경우 어떤 힘이 적용됩니까?
이것은 Pascal의 법률 공식을 사용하여 계산할 수 있습니다.
f =pa
여기,
p =5000 pa =n/m2
a =0.01 m2
대체 값, f =50n
파스칼 법칙의 파생
두께가 rho (ρ) 인 액체에는 임의의 오른쪽 변형 삼각형이 있습니다. 성분이 작기 때문에 각 점은 액체 표면과 동일한 풍부한 것으로 가정됩니다. 중력은이 모든 지점에서 동일합니다.
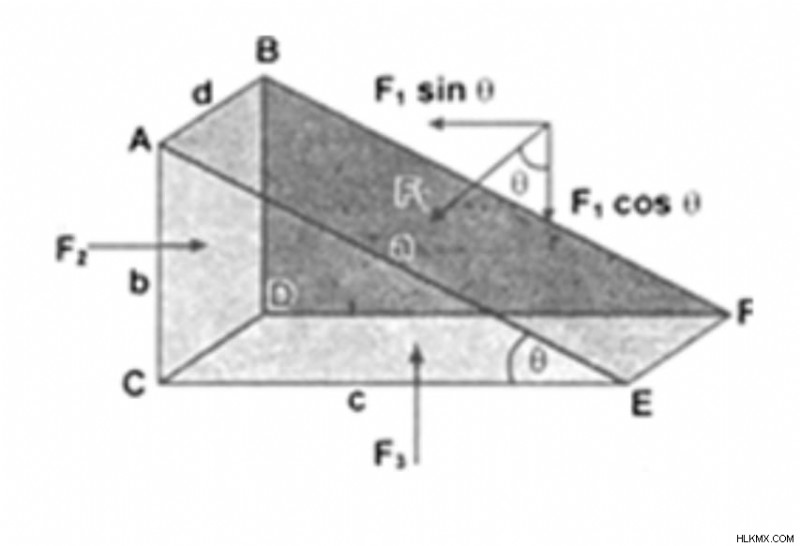
p1, p2 및 p3는 얼굴 ABFE, ABDC 및 CDFE에 전달되는 압력을 나타냅니다.
ab, bd 및 cd는 얼굴 ABFE, ABDC 및 CDFE의 단면 영역입니다.
p1 표면 ABFE에 힘 F1, P2 표면 ABDC에 힘 F2, P3 적용 힘 F3가 개별적으로.
.이런 식으로
f1 =p1 × abfe의 면적
=p1 ad
f2 =p2 × abdc의 면적
=p2 bd
및 f3 =p3 × cdfe
=p3 cd
또한 sin θ =b/a sin θ =c/a
프리즘이 평형 상태에 있으므로 프리즘의 순 힘은 0
가됩니다.f1 sin θ =f2
f1 cos θ =f3
p1 ad ba =p2 bd (방정식 -i)
p1 ad ca =p3 cd (방정식 -II)
에서 (i) 및 (ii),
p1 =p2 및 p1 =p3
∴ p1 =p2 =p3
Pascal 법의 응용
다음은 Pascal의 법칙의 적용입니다 :
-
Pascal의 법칙 사용 다양한 장비가 일상 생활에서 사용되는 다양한 장비가 제조됩니다.
-
유압 잭 및 유압 프레스.
-
차량 제동 시스템, 아르테시아 우물, 워터 타워 및 댐에서 저항력을 높이기위한 유압 브레이크.
-
항공기 유압 시스템 :항공기의 유압 전력 시스템은 Pascal의 법칙을 사용하여 활주로의 비행기 속도를 늦 춥니 다. 또한 비행 제어 메커니즘, 랜딩 기어 등에 사용됩니다.
-
유압 펌프 :자동차 산업에 사용되는 유압 펌프는 파스칼 법의 철학을 사용합니다.
-
가압 탱크의 유압 테스트, 압력 게이지 교정, 올리브, 헤이즐넛 및 해바라기 오일과 같은 오일의 누름, 목재 주식 압축 등
-
치과 의사의 훈련, 잭하메스, 페인트 분무기 및 트럭의 에어 브레이크 등과 같은 다양한 공압 장치 등은 Pascal의 법칙의 원칙에 따라 작동합니다.
결론
생존 가능한 압축 요법의 역학은 파스칼의 법칙에 의해 설명되며,이 법은 닫힌 용기의 유체 (근육 또는 근육 무리)에 압력이 적용될 때 (근막 근육 및 압축 붕대), 컨테이너의 모든 지점마다 동등한 증가가 있습니다. Pascal의 법칙은 자동차 산업에서 사용하는 유압 펌프 제작에 사용됩니다. 또한 올리브 오일 및 헤이즐넛 오일과 같은 프레스 오일, 압력 게이지의 교정 및 Jackhammer 's, Paint Sprayers 및 트럭 브레이크와 같은 장치에서도 널리 적용됩니다. 유압 및 엔지니어링 및 기술에 큰 역할을합니다.
.
회전 반경의 공식은 무엇입니까?
우리가 그 의미를 이해 한 후에, 반경 반경의 공식이 무엇인지 알아야 할 때가?
균일 한 막대의 회전 반경은 어떤 적용의 종류에 따라 질량 중심 또는 다른 축에서 물체의 포인트 질량의 뿌리 평균 제곱 거리입니다.
신체의 자이라디우스 또는 회전 반경은 항상 회전 축을 중심으로합니다. 관성 모멘트가있는 두 지점 사이의 나선 거리로 정의됩니다. 이 지점의 회전 반경을 보면 여행 한 평균 거리를 파악할 수 있습니다.
다음은 균일 한 막대의 회전 반경 측면에서 모멘트 관성에 대한 공식입니다.

알기 위해 회전 반경 단위는 무엇입니까 , 회전 반경은 mm에서 측정된다는 것을 기억하십시오.
M 원자로 구성된 시스템을 고려하십시오. 각각의 질량은 m입니다. 회전의 수직 거리는 피벗에서 R1, R2, R3,… RN으로 표시됩니다.
회전 반경은 신체의 다양한 입자 사이의 뿌리 평균 거리입니다. 회전 축에서 나오고 회전축에서 파생됩니다.
Gyration 응용 분야의 반경 :
- 주위의 물체의 많은 부분을 퍼뜨리는 데 사용되는 방법을 지칭하는 "gyration 반경"이라는 용어가 있습니다.
- 이것은 물체가 휴식 할 때 회전 축에서 특정 질량 지점까지의 거리입니다.
- 2 차원의 회전 범위를 사용하여 단면 구역이 1 차 설계에서 어떻게 퍼지는지를 보여줄 수 있습니다.
- 신체의 질량은 중심점 주위에 원을 형성합니다. 이것은 회전 반경 단위가 무엇인지 아는 데 유용합니다.
를 찾을 때 회전 반경 단위는 무엇입니까 , 회경 반경은 다음과 같이 결정될 수있다
r =√ (IA)
내가 대상의 두 번째 면적이었고 A는 전체 단면 영역입니다.
2 차원 회수 텐서의 스냅 샷이 동일하지 않으면 회전 반경을 사용하여 조각의 견고성을 파악할 수 있습니다. 보통 두 개의 머리가 있습니다 :하나는 더 작은 머리가 있고, 하나는 그 옆에 더 큰 머리가 있습니다. 예를 들어, 더 겸손한 반 피벗은 더 강력한 전체 피벗보다 곡선 크로스 섹션이있는 조각에 잠길 가능성이 높습니다.
회전 반경은 디자인의 중요한 부분이며, 문제의 일정한 그룹을 종종 살펴 봅니다.
회전 반경 사용
회전 반경은 축을 따라 다양한 구조적 형태의 압축 거동을 비교하는 데 사용됩니다. 이 방법을 사용하여 압축 빔 또는 멤버의 좌굴을 예측할 수 있습니다.
회전 반경 (2 차원)은 구조 공학에 사용되어 신체의 질량을 주위로 이동할 때 기둥의 단면적이 어떻게 변하는지를 보여줍니다.
회전 반경 단위 열을 위해? 열의 회전 반경을 사용하여 강성을 추정 할 수 있습니다. 좌굴을 피하려면 2 차원 자이로 스코프 텐서가 각 축에 같은 1 차 모멘트를 가지고 있는지 확인하십시오. 기둥에 타원형 단면이 있으면 반 축소가 버클을 피우는 경향이 있습니다.
회전의 반경은 일반적으로 엔지니어링의 필수 요소로 일반적으로 계산되며, 지속적인 물질의 몸이 일반적으로 연구됩니다.
얇은 막대의 회전 반경 단위는 무엇입니까?
중심을 통과하는 축에 대한 길이 L 및 질량 M의 균일 한 막대의 관성 모멘트 (MOI)는 길이에 90도 각도를 만드는 데 다음과 같이 표시됩니다.

결론
따라서, 우리는 회전 반경과 회전 반경 단위에 대한 자세한 개요를 가지고있었습니다. 간단히 말해서, 회전 중심 측면에서 신체의 중심에서 모든 질량이 집중된 곳까지의 거리입니다. 이것은 요점에 관성의 순간이있을 것임을 의미합니다. 회전 반경과 관성의 관계를 이해하려면 먼저 회전 축을 이해해야합니다. 다른 하나를 알고 있다면 하나를 찾는 것이 간단합니다.