‘and’게이트와‘not’게이트를 계단식으로 a nand 게이트를 구현할 수 있습니다. NAND 게이트에 두 개 이상의 입력이있을 수 있습니다. 그러나 출력은 하나뿐입니다. 또한 부정 및 게이트라고도합니다.
NAND 게이트의 표현은 다음과 같이 쓸 수 있습니다. 
부울 대수학에서 NAND 게이트는 보편적 인 게이트로 간주됩니다. 또한 다른 범용 게이트를 구현하는 데 사용될 수 있습니다. NAND 게이트 의이 속성은 기능적 완전성이라고도합니다.
진실 테이블
2 입력 NAND의 진실 테이블 :
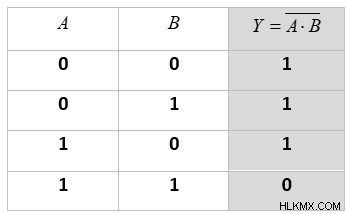
진실 테이블에서 출력이 참이라는 것을 알 수 있습니다 (1) 입력 중 하나 이상이 거짓 인 경우 (0). 모든 입력이 참이면 (1) 출력은 False (0)입니다.
3 입력 NAND 게이트의 진실 테이블은 다음과 같이 표시 될 수 있습니다.
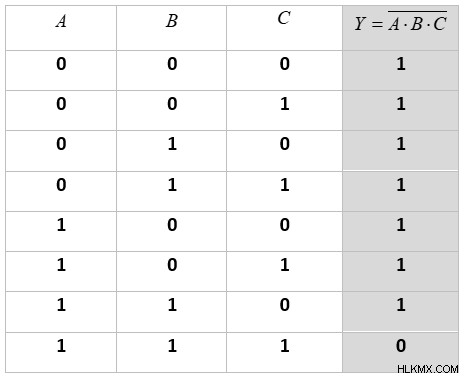
이 테이블에서도 출력이 항상 사실이라는 것을 알 수 있습니다 (1) 입력 중 하나 이상이 거짓 인 경우 (0). 모든 입력이 참이면 (1) 출력은 False (0)입니다.
회로도
and an and gate and gate를 cascading으로 획득 할 수 있으며 다음과 같이 게이트가 아닙니다.
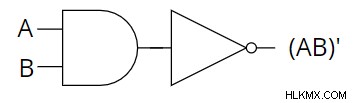
위의 다이어그램에서 및 게이트의 출력이 반전되고 있음을 알 수 있습니다. 별도의 게이트가 아닌 게이트를 추가하는 대신, 우리는 단순히 및 게이트의 출력에 버블을 추가 할 수 있습니다. 기포는 출력에서 반전을 나타냅니다. 따라서 NAND 게이트의 회로 기호는 다음과 같습니다.
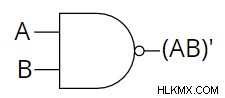
De Morgan의 첫 번째 법에 따르면, 
이 정리에서 우리는 회로를 말할 수 있습니다. 은 회로와 동일합니다. 
따라서 회로 는 다음과 같이 설명 할 수 있습니다
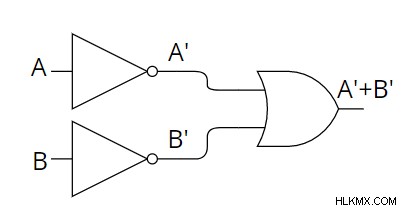
게이트가 아닌 대신 입력에서 기포를 사용할 수 있으며, 다음과 같이 반전을 나타냅니다.
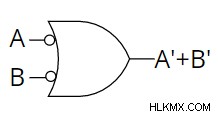
따라서, NAND 게이트와 버블 링 또는 게이트는 동일하다고 말할 수 있습니다.
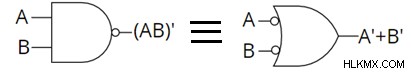
범용 게이트
NAND 게이트는 게이트가 아닌 게이트, 게이트, 게이트, ex-or and ex-nor 게이트를 구현하는 데 사용될 수 있습니다.
게이트 구현
NAND 게이트를 사용하여 게이트가 아닌 게이트를 구현하려면 NAND 게이트의 입력을 묶습니다. 즉, 두 개의 동일한 입력을 제공합니다. 출력 표현식은 다음과 같습니다.
[idempotency의 법칙 사용 
] NAND를 사용하지 않는 구현은 다음과 같이 설명 할 수 있습니다.
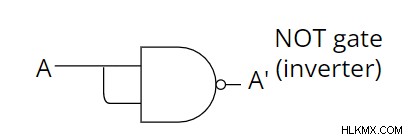
구현 및 게이트
및 게이트를 구현하려면 NAND 게이트의 출력을 반전합니다. 출력 표현식은 다음과 같습니다.
[이중 반전의 속성 사용 
NAND의 구현 및 사용 및 사용은 다음과 같이 설명 할 수 있습니다.
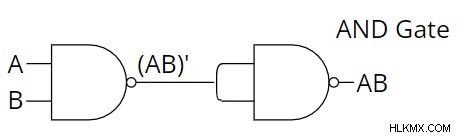
첫 번째 NAND 게이트의 출력이 반전되어 게이트를 얻습니다. 반전은 NAND 게이트를 사용하여 구현 된 NOT GATE를 사용하여 수행됩니다.
구현 또는 게이트
또는 게이트를 구현하려면 NAND 게이트의 입력을 반전합니다. 출력 표현식은 다음과 같습니다.
[De Morgan 법률 사용 
] 
[이중 반전의 속성 사용 NAND의 구현 또는 사용을 다음과 같이 설명 할 수 있습니다.
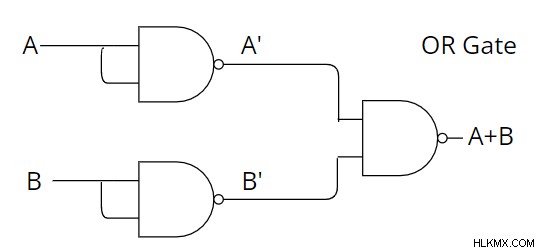
오른쪽의 NAND 게이트에 두 개의 입력이 또는 게이트를 얻기 위해 반전 된 것을 알 수 있습니다.
구현 또는 게이트
NOR 게이트를 구현하려면 입력과 NAND 게이트의 출력을 반전합니다. 출력 표현식은 다음과 같습니다.
[De Morgan 법률 사용 
[이중 반전의 속성 사용 NAND의 구현을 다음과 같이 설명 할 수 있습니다 :
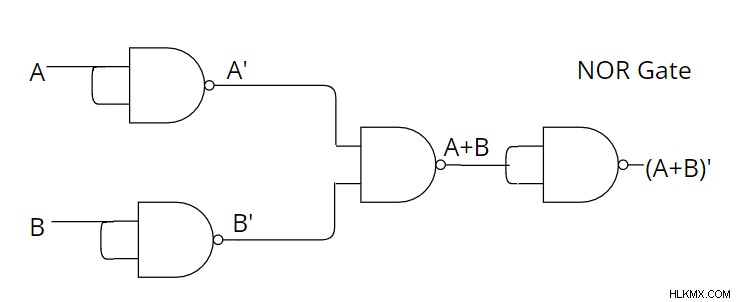
EX-OR 게이트 구현
Ex의 구현 - 또는 NAND를 사용하는 것은 다음과 같이 설명 할 수 있습니다.
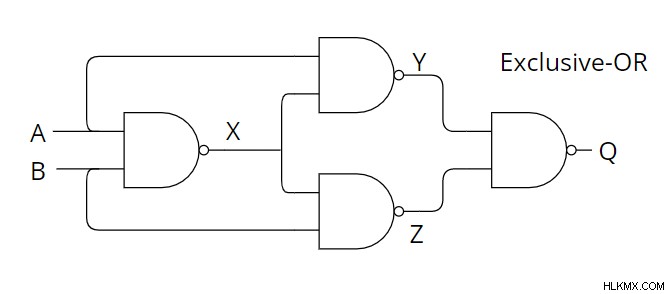위의 다이어그램에서 출력 표현식은 다음과 같이 설명 할 수 있습니다.
[De Morgan 법률 사용 ]
[이중 반전의 특성 사용 ]
[흡수 법 사용 
]
마찬가지로
[De Morgan 법률 사용 ]
[이중 반전의 속성 사용 ]
[흡수 법 사용 ]
마지막으로,
[y and z의 대체 값]
[첫 번째 De Morgan 법칙 사용 ]
[두 번째 De Morgan 법칙 사용 
]
[이중 반전의 속성 사용 ]
ex-nor 게이트 구현
ex의 구현 또는 NAND를 사용하는 것은 다음과 같이 설명 할 수 있습니다.
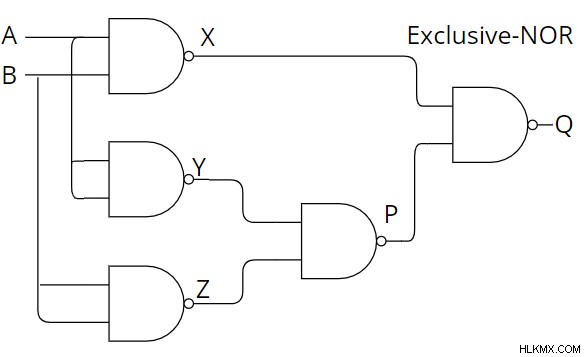
위 다이어그램의 출력 표현식은 다음과 같이 설명 할 수 있습니다.
[idempotency의 법칙 사용 ]
마찬가지로
[idempotency의 법칙 사용 ]
지금,
[y and z의 값을 대체]
[첫 번째 De Morgan 법칙 사용 ]
[이중 반전의 속성 사용 ]
마지막으로,
[x 및 p의 대체 값]
[첫 번째 De Morgan 법칙 사용 ]
[이중 반전의 속성 사용 ]
[두 번째 De Morgan 법칙 사용
결론
NAND 게이트는‘NOT’(n) 게이트와‘및’게이트의 조합에서 얻습니다. NAND 게이트의 출력은 출력은 항상 사실입니다 (1) 입력 중 하나 이상이 거짓 인 경우 (0). 모든 입력이 true 인 경우 (1) 출력은 False (0)입니다.
NAND 게이트는 출력에서 거품 또는 역전을 가진 AN 및 게이트를 사용하여 표현할 수 있습니다. NAND 게이트는 보편적 인 게이트입니다. 즉, XOR 및 Exor 게이트뿐만 아니라 다른 기본 게이트를 구현하는 데 사용될 수 있습니다.
.
