소개
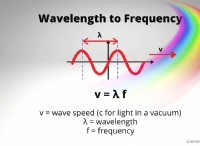
이 법은 일반적으로 Snell의 법이라고합니다. Snell의 법칙은 주어진 색상의 햇빛과 갤러리의 주어진 시도에 대해 굴절 각도의 원형 함수에 대한 발병 각도의 원형 기능의 정량적 관계로 설명됩니다. Snell의 법칙 공식은 다음과 같이 표현됩니다.
n =굴절률
=입사각 및 반사 각도
빛의 행동은 상당히 예측 가능한 것으로 잘 알려져 있습니다. 빛의 광선이 평평한 거울에 접근하고 반사한다면, 반사 된 빛의 행동은 반사 법으로 알려진 예측 가능한 법칙을 따릅니다.
사건 광선은 거울에 접근하는 빛의 광선입니다. 반사 광선은 거울을 떠나는 빛의 광선입니다. 광선이 거울에 영향을 미치는 발생 지점에서 거울 표면에 수직 인 선을 그릴 수 있습니다. 이것은 정상 선이라고합니다. 입사 및 반사 광선에 의해 형성된 각도는 정상 선에 의해 두 개의 동일한 각도로 나뉩니다. 입사각은 입사 빔과 정상에 의해 형성된 각도입니다. 반사 각도는 반사 빔과 정상에 의해 형성된 각도입니다.
굴절 법칙
사고 광선, 반사 광선 및 거울 표면의 정상은 모두 반사의 법칙에 따라 같은 평면에 있습니다. 입사각은 반사 각도와 같습니다.
두 번째 굴절 법칙에 따르면, 한 매체에서 다른 매체의 경계로 돌아 오는 사고 광선이 굴절되면, 발병 각도의 사인의 정량적 관계는 종종 주어진 파장의 선샤인에 대해 일정하다. 스넬의 굴절 법칙.
Optics의 Snell의 법칙은 두 접촉 물질 사이의 경계 또는 분리 표면을 가로 지르는 햇빛의 광선과 모든의 굴절 지수 사이의 관계입니다. 이 법은 1621 년 네덜란드 물리학 자이자 Science Of Science Wellebrord Snell (Snellius라고도 함)에 의해 발견되었습니다. Snell의 법칙에 대한 설명은 Christian Huygens의 Lightweight에 대한 글에서 언급 할 때까지 출판되지 않았습니다. 그림 내에서 N1 및 N2는 2 배 미디어에 대한 굴절 지수를 나타내고, α1 및 α2 제곱은 경계에서 전통적인 (수직) 라인 Nn으로 레이 R이 만드는 발생률 및 굴절 각도를 측정합니다. Snell의 법칙은 n1/n2 =sin α2/sin α1을 주장합니다. 정량적 관계 N1/N2는 주어진 주어진 파장의 햇빛에 대해 일정 할 수 있으며, 두 사인의 정량적 관계는 모든 각도에 추가로 끊임없는 관계가 있습니다. 따라서, 가벼운 광선의 흔적은 전통적인 광선을 향해 구부러진 다. 그리고 햇빛의 광선의 흔적은 가역적이기 때문에, 한 번 더 낮은 굴절 지수의 물질로 나오는 전통적인 곳에서 광선이 구부러졌습니다.
.결론
반사 및 굴절 법칙을 배운 후, 우리는 주어진 반사 표면적 단위에 대한 발생률과 반사 각도가 초점 길이가 1/2임을 거울 표면의 곡률 반경 (r =2F 또는 f =r/2)과 같음을 확인했습니다 (r =2F 또는 f =r/2). 우리는 물의 굴절 지수가 1.33에 관한 것임을 추가로 확인하는 경향이 있으며, 이는 공기보다 물을 통과하는 데 33/3 더 긴 가벼운 중량이 필요하다는 것을 의미합니다. 또한, 우리는 입사각이 전체 내부 반사와 직접 관련되어 있다고 말하는 경향이 있습니다.