임박한 움직임

정적 마찰의 힘을 극복하려는 신체는 임박한 움직임에 있다고합니다. 다른 말로, 임박한 움직임은 몸이 움직이려는 정확한 순간입니다. 마찰의 두 가지 유형이 있습니다 :정적과 운동. 신체가 이완되면 정적 마찰이 발생합니다. 마찰력은 몸에 작용하는 순 힘을 취소합니다. 마찰은 정렬 된 힘이 아니기 때문에 고정 방향이 없습니다. 그것은 두 Bodie의 상대 운동에 반대하여 행동 할 수있는 벡터 수량입니다. 한 몸체가 제공하는 마찰력은 다른 몸에 의해 시도 된 운동의 반대 방향으로 발생합니다.

미끄러짐

특정 시스템에서 특정 접촉 표면 동안 슬라이딩에 LED가 LED. 다가오는 움직임은 마찰력 F와 적용된 하중 N이 F =µSN과 같이 서로 비례하는 매체에서 발생한다는 것을 기억하십시오. 마찰 시스템의 다가오는 움직임이 미끄러지거나 한 쌍의 인터페이스 표면이 끊어짐에 따라 발생할 수있는 다른 유형의 문제를 살펴볼 것입니다. 포인팅은 두 번째 상황을 설명하는 데 사용됩니다.

프레스 힘이 계속 증가하면 상자가 마침내 움직이기 시작합니다. 상자가 미끄러지기 시작하면 상자의 움직임에 저항하는 일종의 마찰은 정적 마찰에서 운동 마찰로 이동합니다. 임박한 움직임은 상자가 미끄러지기 직전에 순간을 나타냅니다. 이것은 미끄러지기 전에 적용 할 수있는 최대 정적 마찰력이라고도합니다. 최대 정적 마찰력은 상자와 표면에 작용하는 정상 힘을 곱한 정적 마찰 계수와 동일합니다.

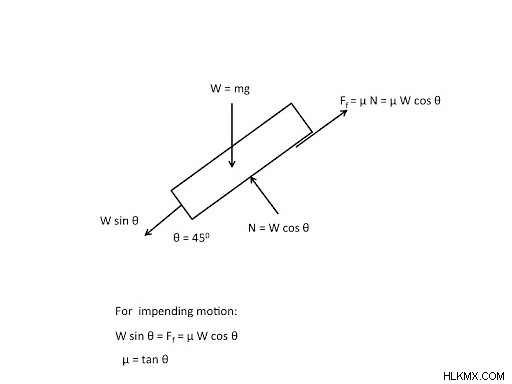
미끄러짐 가장자리에있는 몸체의 상태를 임박한 움직임이라고합니다. 그러한 경우, 정적 마찰은 최대 값을 달성했으며, 이는 방정식을 사용하여 계산할 수 있습니다.

f =µs n

마찰력은 일반적으로 재료 사이의 상대 운동의 반대 방향으로 작용합니다. 적용된 하중 (P)이 상승하면 마찰력 (F)이 F

임박한 움직임의 의미를 더 잘 이해하기 위해 다음 부분의 정적 간 변환의 세 단계를 살펴 보겠습니다.

3 개 영역에서 정적에서 움직임으로 전환

미끄러짐 또는 다가오는 움직임이 움직일 때까지 영역이 움직이지 않을 것입니다. 상태가 평형 상태 인 한,이 단계의 마찰력은 평형 방정식으로 설명됩니다. f
임박한 움직임 - 이것은 신체가 떨어질 때입니다. 정적 마찰은이 시점에서 최대 값을 달성합니다. 마찰력은 접촉중인 표면의 주어진 조합에 대한 공식에 의해 제공됩니다.

f =fmax =µs n

본문은이 단계에서 적용된 힘의 방향으로 속도를 높입니다. 마찰력은이 시점에서 동역학 마찰로 불리는 덜 값으로 줄어 듭니다. 마찰력은 방정식을 사용하여 계산할 수 있습니다.

f =fmax =µk n

매체에서 떨어지는 지점에있는 항목의 상태는 다가오는 움직임으로 설명됩니다. 정적 마찰이 최대 한계에 도달하면 방정식 F =µs N을 사용하는 것으로 추정 될 수 있습니다. 다가오는 동작이 발생합니다. 마찰은 품목이 휴식 위치에서 이동할 때 접촉 표면에서 미끄러지는 방향을 제한합니다. 운동에 접근하는 방향으로도 알려진이 방향을 결정하려면 마찰 부족으로 시스템이 어떻게 흐를 수 있는지 조사하십시오. 우리는 임박한 모션이 어떤 임박한 모션에 수반되는지 더 잘 이해하기 위해 임박한 움직임을 포함하여 정적으로 모션 변환의 세 영역을 살펴볼 것입니다.

MCQS

진폭이 정상 반응에 비례하는 정적 마찰력이있는 움직임은 무엇입니까?

실제 모션
임박한 모션
둘 다 a. 그리고 b.
위의

물질 임박한 움직임은
에 의해 중단됩니다

슬라이딩 마찰
롤링 마찰
정적 마찰
동역학 마찰

를 염두에두고 가리키는 지적

어떤 매체에서 떨어지는 지점의 객체 상태는 다가오는 움직임에 의해 설명됩니다.
따라서 정적 마찰이 최대 값에 도달하면 임박한 움직임이 발생합니다.
기호 µk는 운동 마찰 계수를 나타냅니다. 반면 마찰 계수는 같은 방식으로 사용됩니다.
신체를 휴식 위치에 유지하는 힘은 정적 마찰이라고합니다.
작동하려면 몸이 정적 마찰에 저항해야합니다.
또한, 본체의 최대 정적 마찰은 µs의 정상 힘의 µs에 해당합니다.

결론 :

임박한 움직임은 매체에서 미끄러질 직전에있는 물체가있을 때 움직임의 형태를 설명합니다. 다가오는 움직임은 정적 마찰이 가장 큰 한계에 접근 할 때 발생합니다. 물건이 자체 휴식 위치에서 미끄러질 준비가되면 마찰은 항상 상호 작용 표면에서 미끄러지는 방향에 저항합니다. 임박한 움직임의 방향으로 알려진이 방향을 확립하기 위해 마찰 부족으로 시스템이 어떻게 흐르는 지 분석합니다.