1. 속도와 시간 사용 :
* 일정한 가속도 : 속도가 변경된 초기 속도 (v₀), 최종 속도 (V) 및 시간 간격 (t)을 알고 있다면 다음 방정식을 사용할 수 있습니다.
```
가속도 (a) =(v -v₀) / t
```
* 정식 가속도 : 가속도가 일정하지 않은 경우 미적분학을 사용해야합니다. 시간에 따라 속도 함수의 미분을 취하여 가속도를 찾을 수 있습니다.
2. 변위 및 시간 사용 :
* 일정한 가속도 : 초기 속도 (v₀), 변위 (ΔX) 및 변위가 발생한 시간 간격 (t)을 알고 있다면 다음 방정식 중 하나를 사용할 수 있습니다.
```
Δx =v₀t + (1/2) at²
```
또는
```
v² =v +² + 2aΔx
```
그런 다음 가속도 (a)를 해결할 수 있습니다.
* 정식 가속도 : 변위 기능에 대한 자세한 정보가 필요합니다. 이 경우 미적분학을 사용해야 할 수도 있습니다.
3. 중력 사용 :
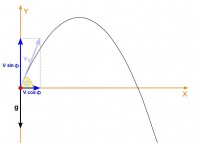
* 중력의 영향으로 물체가 이동하는 경우 중력 (g)으로 인해 가속도를 알려진 값으로 종종 사용할 수 있습니다. 지구상에서 G는 약 9.8m/s²입니다.
예 :
자동차가 휴식에서 시작하여 (v₀ =0m/s) 5 초 안에 20m/s의 속도에 도달한다고 가정 해 봅시다. 가속도를 찾을 수 있습니다.
```
a =(v -v -)/t =(20 m/s -0 m/s)/5 s =4 m/s²
```
중요한 메모 :
* 방향 : 가속도는 벡터 수량이므로 크기와 방향이 모두 있습니다. 가속을 계산할 때 운동 방향을 고려하십시오.
* 단위 : 모든 장치가 일관성이 있는지 확인하십시오. 예를 들어, 속도와 초에 초당 미터 (m/s)를 시간 동안 초당 미터 (m/s)를 사용하는 경우 가속은 초당 정사각형 (m/s²)입니다.
* 일정한 가속도 : 위의 방정식은 가속도가 일정한 상황에만 유효합니다. 가속도가 시간이 지남에 따라 변경되는 경우 미적분학을 사용하여 찾아야합니다.
특정 시나리오를 염두에두고있는 경우 알려 주시면 작업을 수행하는 데 도움을 줄 수 있습니다!