삼투압 - 정의, 공식, 예

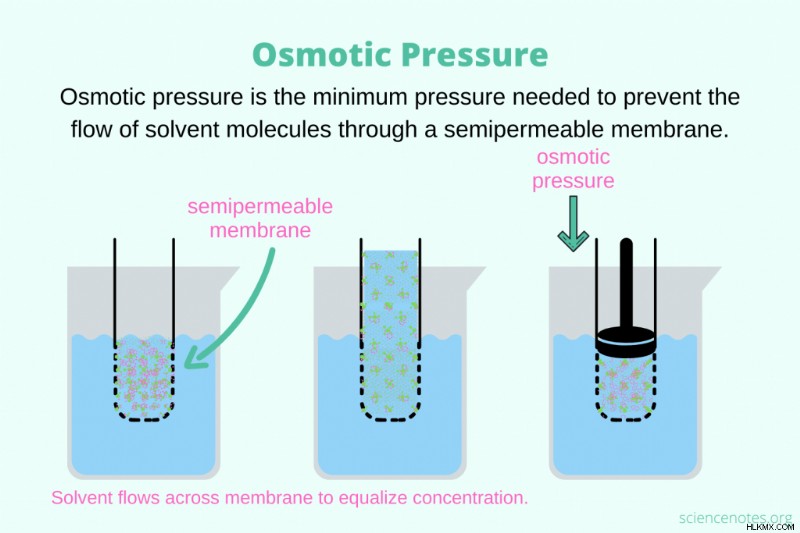
삼투압 용매 분자 (물)가 반투과성 막을 통해 흐르는 것을 방지하는 최소 압력입니다. 다시 말해, 막의 양쪽에 용액의 농도를 평등하게하는 반투과성 막에 대한 용매의 압력이다. 삼투압은 물질의 공동 특성이므로 화학적 동일성이 아닌 용질 입자의 수에 따라 다릅니다.

삼투압이란 무엇입니까? 작동 방식

삼투압은 확산과 삼투의 예입니다. 확산에서, 분자는 용질 및 용매 둘 다가 골고루 분산 될 때까지 고농도의 영역에서 저농도의 영역으로 이동한다. 삼투에는 용매 분자 이동을 허용하는 반투과성 막이 있지만 더 큰 용질 분자의 전달을 금지합니다.

반투과성 막을 사용하여 순수한 용매 또는 희석 용액 및 농축 용액을 분리하면 물이 막을 가로 질러 흐릅니다. 용매의 움직임은 농도가 양쪽에서 동일 할 때까지 계속됩니다. 따라서 삼투압을 막을 가로 질러 농축 용액으로 밀리는 용매 분자의 힘으로 삼투압을 볼 수 있습니다. 물이 막을 가로 지르는 것을 방지하기 위해 해당 용액에 적용해야합니다.

삼투압 예

다양한 용액의 적혈구는 큰 삼투압의 예입니다. 세포막은 반투과성 막입니다.

적혈구를 물에 넣으면 물이 hypotonic 입니다. 또는 세포 함량과 비교하여 집중적이지 않은 경우. 세포 외부의 물은 세포막을 통해 밀린다. 세포가 부풀어 오르고 터졌습니다.
동위 원소에 적혈구를 배치합니다 솔루션 (예 :생리 식염수)은 세포의 크기 또는 외관에 변화가 없습니다. 물은 동일한 속도로 세포로 들어가서 종료합니다.
농축액에 적혈구를 배치하면 액체는 hypertonic 입니다. 또는 세포 세포질보다 더 농축 된. 물은 세포를 빠져 나와 축소되고 구겨진 외관 (crenation)을 제공합니다.

계란을 사용하여 삼투압의 영향을 입증 할 수 있습니다. 먼저, 날걀을 식초 나 약한 아세트산에 담그고 껍질을 녹입니다. 이것은 반투과성 막이 노른자와 계란을 둘러싸고 있습니다.

계란을 옥수수 시럽에 넣으십시오. 시럽에는 설탕이 많지만 물은 거의 포함되어 있으므로 계란 함량과 관련하여 과도 적입니다. 물은 계란에서 시럽으로 막을 가로 질러 흐릅니다. 계란은 줄어들면서 눈에 보이는 노른자 만 남겨 둡니다.
계란을 순수한 물에 넣으십시오. 물은 계란 함량과 관련하여 저혈압이므로 물은 막을 달걀로 가로 질러 부풀어줍니다.

삼투압 공식

삼투압 공식에 대한 크레딧은 Jacobus van't Hoff로갑니다. 이 공식은 삼투압과 용질 농도와 관련이 있습니다.

π =imrt

여기서 π는 삼투압이고, 나는 반도가 아닌 인자, m은 용질 어금니 농도, r은 이상적인 가스 상수, t는 절대 온도입니다.

예제 문제

예를 들어, 포도당의 양 (c ₆ H ₁₂ o ₆ ) 물 1 리터당 등방성 혈액 (37 ° C에서 7.64 atm) 인 정맥 용액이 필요합니까?

첫 번째 단계는 Van't Hoff 요소를 결정하는 것입니다. 포도당은 물에 용해되지만 이온으로 분리되지는 않습니다. 따라서 Van't Hoff Factor는 1입니다.
다음으로 섭씨 온도를 절대 온도 (켈빈)로 변환하십시오. 절대 온도는 37 + 273 =310 켈빈입니다.
이제 포도당의 농도를 계산하십시오.

여기에는 삼투압 공식을 재 배열하는 것이 포함됩니다 :

π =imrt
M =π/irt =7.65 atm/(1) (0.08206 l · atm/mol · k) (310) =0.301 mol/l

용액의 각 리터마다 0.301 몰의 자당이 있습니다.

포도당의 몰 질량을 찾으십시오. 주기율표에서 :

C =12 g/mol
H =1 g/mol
O =16 g/mol

포도당 공식 사용 (c ₆ H ₁₂ o ₆ ), 몰 질량은 :

입니다

어금니 질량 포도당 =6 (12) + 12 (1) + 6 (16) =72 + 12 + 96 =180 g/mol

용액을 만들기 위해 필요한 포도당의 질량은 어금니 질량에 포도당의 질량을 곱한 것입니다.

포도당 질량 =0.301 mol x 180 g/mol =54.1 그램

용액의 다른 용질은 삼투압에도 영향을 미칩니다. 이 예에서, 용액은 순수한 물에서 포도당이 아닌 생리 식염수에서 포도당 일 가능성이 높다.

참조

Atkins, Peter W.; De Paula, Julio (2010). "섹션 5.5 (e)". 물리 화학 (9th ed.). 옥스포드 대학 출판부. ISBN 978-0-19-954337-3.
Lewis, Gilbert Newton (1908). "농축 솔루션의 삼투압과 완벽한 솔루션의 법칙". 미국 화학 학회지 저널 . 30 (5) :668–683. doi :10.1021/ja01947a002
Voet, 도널드; Judith Aadil; 샬럿 W. 프랫 (2001). 생화학의 기초 (Rev. Ed.). 뉴욕 :와일리. ISBN 978-0-471-41759-0.