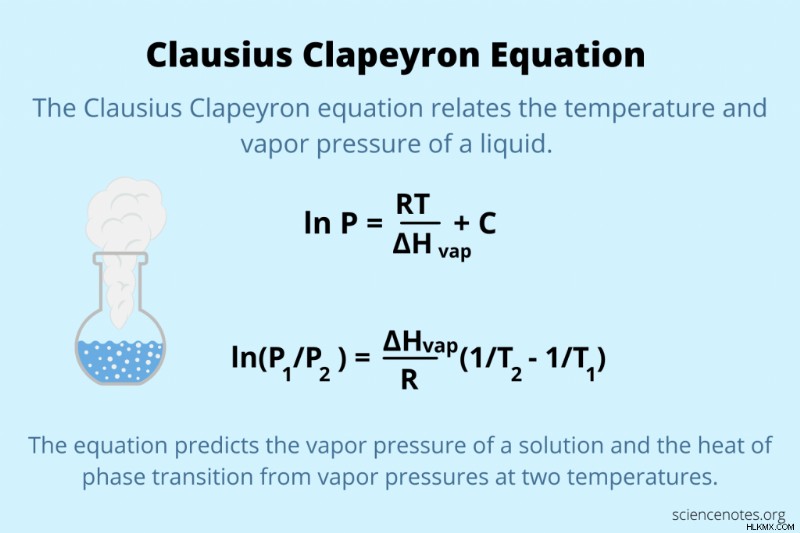
Clausius Clapeyron 방정식 물질의 액체와 증기 상 사이의 위상 전이를 설명하는 관계입니다. 방정식의 형태에 따라 액체의 증기압 또는 두 온도에서 증기 압력으로부터의 기화 열을 예측합니다. 다른 용도는 특정 조건에서 위상 전이가 발생하는지 여부를 예측하는 것입니다.
전제는 대부분의 액체의 기화 곡선이 비슷한 모양을 가지고 있다는 것입니다. 특정 범위에서 온도의 함수로서 증기 압력의 변화는 거의 선형 관계입니다. 다시 말해, 온도가 증가함에 따라 증기 압력이 증가합니다.
이 방정식은 Rudolf Clausius와 Benoît Paul émile Clapeyron의 이름을 따릅니다. 그것은 또한 Clapeyron 방정식 또는 Clausius-Clapeyron 관계라고도합니다. 어떤 이름을 선택하든 방정식은 물리 화학, 열역학 및 기상학에 사용됩니다.
Clausius Clapeyron 방정식 공식
Clausius Clapeyron 방정식에는 몇 가지 동등한 형태가 있으며, 이는 미분 방정식 인 일부 형태를 포함합니다. 그러나 가장 일반적인 형태는 단순히 기화, 온도 및 증기 압력의 열 또는 하나의 화학 물질에 대한 증기 압력 및 해당 온도와 관련이 있습니다.
ln p =rt/ Δh vap + c
ln p =- ΔH vap /rt + c
ln (p 1 /p 2 ) =ΔHVAP/R (1/t 2 - 1/t 1 )
ln (p 1 /p 2 ) =- ΔHVAP/R (1/t 1 - 1/t 2 )
ln (p 2 /p 1 ) =- ΔHVAP/R (1/t 2 - 1/t 1 )
여기서, p는 증기 압력이고, R은 이상적인 가스 상수 (0.008314 kj/k · mol), ΔHVAP는 물질의 기화 열, t는 절대 온도 (켈빈에서)이며 C는 일정하다.
.액체의 기화의 어금니 엔탈피는 항상 양수이므로 Clausius Clapeyron 방정식은 온도가 증가함에 따라 증기 압력이 항상 증가 함을 예측합니다. 기화의 엔탈피가 온도에 따라 약간 변하기 때문에 전체 기화 곡선에서 방정식을 사용할 수 있지만 예측은 실험 값에서 벗어납니다.
.Clausius Clapeyron 방정식 예제 문제
예를 들어, 우리는 용액의 증기 압력을 예측하기 위해 Clausius Clapeyron 방정식을 사용할 수 있습니다. 증기 압력이 14.7 ° C에서 10.0 Torr이고 기화 열이 47.2 kJ/mol 인 경우 52.8 ° C에서 1- 프로판올의 증기압을 계산하십시오.
.첫 번째 단계는 단위를 변환하여 방정식에서 작동하는 것입니다. 섭씨 온도를 켈빈으로 변환 :
t k =° C + 273.15
t 1 =14.7 ° C + 273.15
t 1 =287.85 k
t 2 =52.8 ° C + 273.15
t 2 =325.95 K
다음으로 Clausius Clapeyron 방정식을 바르고 p 2 를 해결하십시오. :
ln (p 1 /p 2 ) =ΔHVAP/R (1/t 2 - 1/t 1 ))
ln [10 torr/p 2 ] =(47.2 kj/mol/0.008314 kj/k · mol) [1/325.95 K - 1/287.85 K]
ln [10 torr/p 2 ] =5677 (-4.06 x 10)
ln [10 torr/p 2 ] =-2.305
방정식의 양쪽의 안티 로그를 가져옵니다 :
10 torr/p 2 =0.997
p 2 /10 Torr =10.02
p 2 =100.2 Torr
방정식을 고체에 적용
Clausius Clapeyron 방정식을 사용한 대부분의 계산에는 액체와 증기 상 사이의 위상 전이가 포함됩니다. 그러나 방정식은 또한 승화에도 적용됩니다.
예를 들어, 268K 및 273 K에서의 얼음 압력이 각각 2.965 및 4.560 Torr 인 경우 얼음의 승화에 대한 엔탈피의 열을 추정하십시오.
ΔHSUB =r ln (p 2 / p 1 )/(1/t 1 - 1/t 2 ))
ΔHSUB =r ln (p 273 / p 268 )/(1/268 - 1/273)
ΔHSUB =(0.008314 kJ/k · mol) ln (4.560/2.965)/(1/268 - 1/273)
ΔHSUB =52.370 kJ/mol
참조
- Callen, H.B. (1985). 열역학 및 온도 조절 방지 소개 . 와일리. ISBN 978-0-471-86256-7.
- Clapeyron, M.C. (1834). “Mémoire Sur La Puissance Motrice de la Chaleur”. Journal de l 'école Polytechnique (프랑스어로). 23 :153–190.
- Clausius, R. (1850). “ueber die bewegende kraft der wärme und die gesetze, welche sich daraus für die wärmelehre selbstableiten lassen”[열의 동기력과 열의 이론과 관련하여 추론 할 수있는 법률]. Annalen der Physik (독일어). 155 (4) :500–524. doi :10.1002/andp.18501550403
- Iribarne, J.V.; Godson, W.L. (2013). “4. 수상 시스템 § 4.8 Clausius – Clapeyron 방정식”. 대기 열역학 . 뛰는 것. ISBN 978-94-010-2642-0.
- Wark, Kenneth (1988) [1966]. "일반화 된 열역학적 관계". 열역학 (5th ed.). 뉴욕, 뉴욕 :McGraw-Hill, Inc. ISBN 978-0-07-068286-3.
- yau, m.k.; Rogers, R.R. (1989). 클라우드 물리학의 단기 코스 (제 3 판). Butterworth – Heinemann. ISBN 978-0-7506-3215-7.