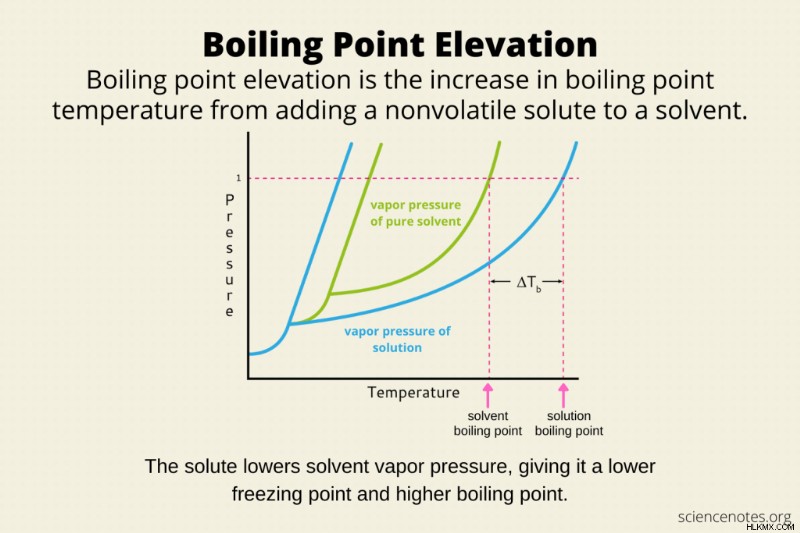
끓는점 고도 비 휘발성 용질을 그것에 용해시킴으로써 용매의 끓는점의 증가이다. 예를 들어, 물에 소금을 용해시키는 것은 물의 끓는점을 높이어 100 ° C보다 높습니다. 동결 지점 우울증과 삼투압과 마찬가지로, 비등점 고도는 물질의 공동 특성입니다. 다시 말해, 효과는 용질의 특성이 아닌 용매에 얼마나 많은 용질 입자가 용해되는지에 달려 있습니다.
비등점 고도가 작동하는 방법
용매에 용질을 용해시키는 것은 용매 위의 증기압을 낮 춥니 다. 끓는 것은 액체의 증기압이 그 위의 공기의 증기 압력과 동일 할 때 발생합니다. 따라서 분자에게 액체에서 증기 상으로 전이 할 수있는 충분한 에너지를 제공하려면 더 많은 열이 필요합니다. 다시 말해, 끓는 것은 더 높은 온도에서 발생합니다.
이유 이것은 용질 입자가 휘발성이 아니기 때문에, 주어진 시간에 그들은 기체가 아닌 액체상에있을 가능성이 높기 때문입니다. 끓는점 고도는 또한 휘발성 용매로 발생합니다. 용질이 용매를 희석하기 때문입니다. 추가 분자는 용매 분자 사이의 상호 작용에 영향을 미칩니다.
전해질은 끓는점 상승에 가장 큰 영향을 미치지 만 용질의 특성에 관계없이 발생합니다. 염, 산 및 염기와 같은 전해질은 용액으로 이온으로 분해됩니다. 용매에 입자가 많을수록 끓는점에 미치는 영향이 커집니다. 예를 들어, 설탕은 염 (NaCl)보다 효과가 적으며, 이는 염화 칼슘보다 효과가 적습니다 (CACL 2 ). 설탕은 용해되지만 이온으로 분리되지 않습니다. 염화 칼슘이 3 개의 입자 (1 Ca 및 2 개의 Cl)로 분해되는 반면, 염화 칼슘은 2 개의 입자 (Na 및 Cl)로 끊어집니다.
유사하게, 더 높은 농도의 용액은 더 낮은 농도 중 하나보다 끓는점이 높다. 예를 들어, 0.02 M NaCl 용액은 0.01 M NACL 용액보다 높은 비등점을 갖습니다.
비등점 고도 공식
비등점 공식은 용매의 정상 끓는점과 용액의 끓는점 사이의 온도 차이를 계산합니다. 온도 차이는 끓는점 고도 상수 입니다 (k b ) 또는 ebullioscopic constant , 몰랄 용질 농도를 곱한다. 따라서 끓는점 고도는 용질 농도에 직접 비례합니다.
Δt =k b · m
비등점 공식의 또 다른 형태는 Clausius-Clapeyron 방정식과 Raoult의 법칙을 사용합니다.
Δt b =molality * k b * i
여기, 나는 반도가 아닌 요소입니다. Van't Hoff 인자는 용질 몰당 용액에있는 입자의 두더지 수입니다. 예를 들어, 설탕이 녹지 만 해리되지 않기 때문에 물에서 수 크로스에 대한 반 아니오 호프 인자는 1입니다. 물에서 소금과 염화칼슘의 반도가 아닌 요인은 각각 2와 3입니다.
참고 :비등점 높이 공식은 희석 솔루션에만 적용됩니다! 집중 솔루션에 사용할 수는 있지만 대략적인 답 만 제공합니다.
비등점 고도 상수
비등점 고도 상수는 1 몰랄 용액의 끓는점의 변화 인 비례 적 요인이다. k b 용매의 특성입니다. 그 값은 온도에 따라 달라 지므로 값 표에는 온도가 포함됩니다. 예를 들어, 일반적인 용매에 대한 비등점 고도 상수 값은 다음과 같습니다.
| 솔벤트 | 정상 비등점, C | k b , c m |
| 물 | 100.0 | 0.512 |
| 벤젠 | 80.1 | 2.53 |
| 클로로포름 | 61.3 | 3.63 |
| 아세트산 | 118.1 | 3.07 |
| 니트로 벤젠 | 210.9 | 5.24 |