시그마 분자 궤도에서 전자 분포는 탄소 카본 (C-C) 결합의 핵혈대 축소 주변에서 균형을 이룹니다. 따라서 C-C 단일 본드 주위에서 자유 회전을 허용합니다. 우주에서 탄소 원자의 3 차원 배열은이 회전으로 인해 관찰되며, 이러한 원자는 서로 변할 수 있습니다.
.이러한 수소와 탄소 원자의 3 차원 배열은 C-C 결합 주위의 회전 과정에 의해 서로에 의해 쉽게 변형 될 수 있으며, 구성 요소, 또는 로타미터로 쉽게 변형 될 수 있습니다. 그러나, 반발 상호 작용으로 인해, 이러한 회전은 C-H 결합의 구름 전자 사이에서 자유롭지 않다. 이 유형의보다 반발하는 상호 작용은 비틀림 균주로 알려져 있습니다.
형태 이성질체
에탄의 예와 일치하는 기본 사항을 이해합시다.
형태 이성질체는 단일 결합 주위의 회전 과정에 의해 이성질체의 상호 연결이 일어날 수있는 입체 소성기의 한 유형입니다. 이 과정에서 회전 에너지는 단일 결합 유형의 회전의 경우에만 장벽으로 작동합니다. 한 유형의 순응자를 다른 유형으로 상호 연결하는 데 극복해야합니다. 구조적 이성질체가 발생하기 위해서는 에너지의 장벽이 작아야합니다. 구조적 이성질체는 에탄과 부탄과 같은 다양한 유형입니다.
우리는 이러한 형태 이성질체를 두 가지 주요 사례로 광범위하게 분류 할 수 있습니다 :
이클 로트 형식 :이것은 수중 아톰이 서로 가장 가까운 방법으로 연결된 방법으로 배열되는 형태의 유형입니다.
순응 자의 안정성에 영향을 미치는 요인 중 일부는 다음과 같습니다.
각도 변형 :이 유형의 변형률은 일반적으로 순환 구조를 나타내지 만 주기적 구조에는 존재하지 않습니다. 정상적인 유형의 각도와의 편차는 각도 변형과 함께합니다.
van der waals 변형 :멀리 떨어져있는 비 결합 원자 그룹은 반발이있을 때 반란이 van der waals 변형으로 알려져 있습니다.
. 비틀림 균주 및 입체 변형
뉴먼 투영에서 우리는 안티, 가우 치 및 기타 형태의 에너지를 연구합니다. Gauche 및 Eclipsing 그룹은 Steric 균주 또는 비틀림 균주의 형태를 불안정화합니다. 입체 방해물은 광범위한 개념이며, 원자 그룹이 서로 매우 가까울 때 얻어지며 전자 구름의 반발로 인한 에너지가 갑자기 증가합니다.
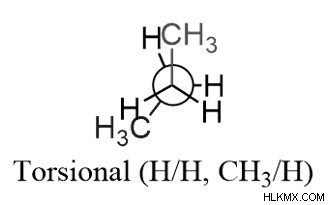
.비틀림 변형은 주로 일식 그룹에서 비롯됩니다. 근처의 탄소의 일식 그룹으로부터 에너지의 양이 증가하는 것은 일식 그룹의 비틀림 상승으로 알려져있다.
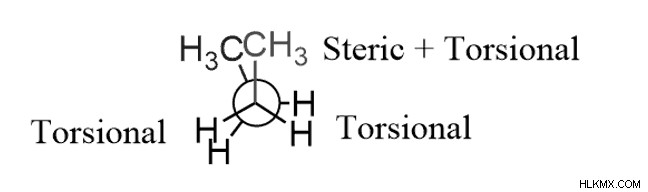
두 균주, 비틀림 및 Steric의 존재, 두 개의 큰 그룹의 일식 결과 :
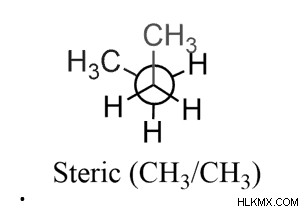
두 가구 그룹의 상호 작용은 항상 입체적 인 방해물입니다. 가우 쉐 형태는 서로 가까운 더 큰 그룹과 관련이있는 입체 변형으로 인한 방지 변형과 비교할 때 높은 에너지로 인해 항상 덜 안정적입니다. (60o vs 180o).
결론
시그마 분자 궤도에서 전자의 분포는 C-C 결합의 핵 축 주위에 균형을 이룹니다. 따라서 C-C 단일 본드 주위에서 자유 회전을 허용합니다. 우주에서 탄소 원자의 3 차원 배열은이 회전으로 인해 관찰되며,이 원자들은 서로 변할 수 있습니다.
.형태 이성질체는 단일 결합 내에서 회전에 의해 이성질체의 상호 연결이 일어난 일종의 입체 소성기입니다. 이 과정에서 회전 에너지는 단일 결합 유형의 회전의 경우에만 장벽으로 작동합니다. 순응 자의 안정성에 영향을 미치는 몇 가지 요인은 반 데르 발스 균주, 입체 변형, 비틀림 변형 및 각도 변형입니다.
관련 페이지
| JEE 알림 | Jee Study 자료 |
| jee 간의 차이 | JEE 중요한 공식 |
| JEE 시험 팁 | Jee Full Forms |
| 뿌리 평균 제곱 속도 | 방사형 및 각도 노드 공식 |
| d- 블록 요소의 자기 특성 | Arrhenius 이론의 한계 |
| nernst 방정식 및 응용 프로그램 | 유화 이론 |