함수의 미분은 해당 함수의 특정 지점에서 초기 기능의 변화 속도를 알려주는 함수입니다. 기능의 미분을 초기 함수의 출력이 입력의 작은 변화에 얼마나 민감한지를 측정하는 것으로 생각할 수 있습니다. 파생물은 주어진 시점에서 기능이 얼마나 빨리 변경되고 있는지 알려줍니다. 따라서 파생 상품은 변위, 속도 및 가속도와 같은 변화율과 관련된 모델링 상황에 유용합니다.
함수의 미분 :
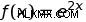
e 형태로 함수의 미분을 찾기위한 특별한 규칙에 의해 결정될 수있다. 일반적인 규칙은 다음과 같습니다.
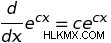
따라서이 규칙을 사용하여 다음을 결정할 수 있습니다.
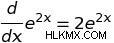
즉, 함수 ƒ (x) = e 의 미분 ƒ '(x) =2 e 입니다 . 이 파생물은 입력 변경 당 원래 함수의 출력을 변경 속도를 알려줍니다. 기본적으로 두 방정식은 함수의 출력 ƒ (x) = e 임을 알려줍니다. 2 e 의 계수만큼 자랍니다 입력 당. 따라서 x 값이 하나라면 해당 값을 방정식에 꽂을 수 있습니다.
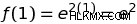
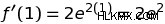
이 방정식은 우리에게 두 가지를 알려줍니다. 첫째, x =1 지점에서 함수 ƒ (x)는 e 의 출력을 갖습니다. . 둘째, 파생물은 x =1 지점에서 ƒ (x)의 출력이 2 e 의 계수만큼 변화하고 있음을 알려줍니다. .
미분은 무엇입니까?
앞에서 언급 한 바와 같이, 함수의 미분은 함수의 출력이 입력의 변화에 얼마나 민감한지를 측정 한 것입니다. ƒ (x)의 미분은 x의 변화와 관련하여 ƒ (x)의 출력 변화 속도를 측정합니다.
선형 방정식 y 가있는 간단한 경우를 상상해보십시오. =2x+3. 또한,이 라인에 떨어지는 두 세트의 X Y 좌표를 선택할 수 있습니다 :(1,5) 및 (2,7). 이 두 지점 사이의 X와 관련하여 함수의 변화 속도는 얼마입니까? 컴퓨팅으로 이것을 알아낼 수 있습니다.
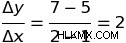
이것은이 두 점 사이에서 함수의 출력이 2의 계수로 변경되고 있음을 의미합니다. =2 x +3.
실제로, 방정식 y 의 두 점에 대해 =2x+3, 변화율은 항상 2 일 것입니다. 이것은 우리의 함수의 모든 지점에서 함수의 출력이 x에 대해 2의 계수로 증가하고 있음을 의미합니다. 또한 이것은 파생 상품을 찾는 첫 번째 규칙을 제공합니다. ƒ (x)가 선형 함수 y =입니다. mx+ b :
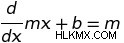
즉, y = 형태의 선형 함수에 대해 mx+ b , 그 함수의 미분은 기울기 m 와 같습니다. . X의 변화와 관련하여 Y의 일부 변화 속도를 표현하는 선형 방정식에 대해 생각하면 함수의 기울기 m 각 입력에 대해 출력 변경 속도가 2의 계수로 변경 속도를 제공합니다.
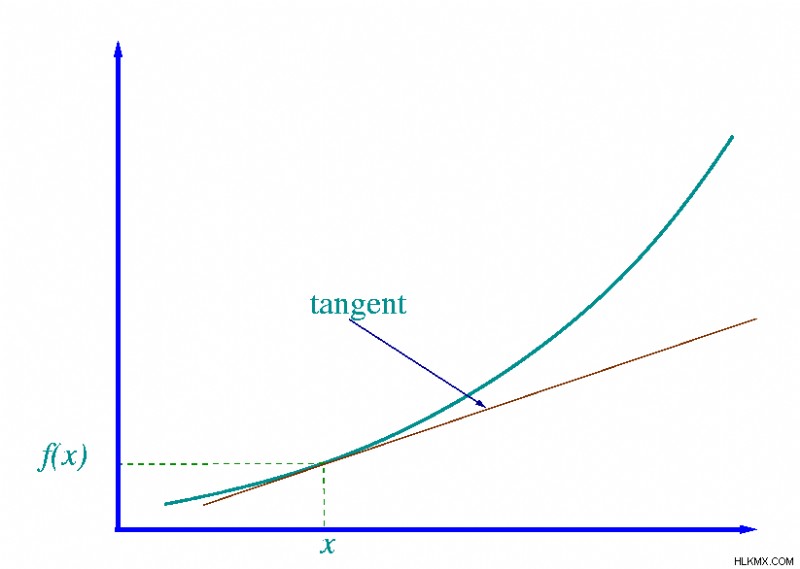
.더 높은 정도의 함수 (예 :x, x)에 대한 파생물을 찾는 과정은 두 지점 사이의 기울기를 찾는이 과정을 일반화하고 Δx가 임의로 작아짐에 따라 Δy/Δx 비율을 제한 값을 발견합니다. 결과적으로 어느 시점에서 함수의 미분은 본질적으로 단일 지점에서 그래프의 기울기를 알려줍니다. 이것은 또한 어느 시점에서 함수의 미분이 그 시점에서 그래프에 접하는 선의 기울기를 제공한다는 사실에서도 볼 수 있습니다.
.좋아, 그게 다 좋고 좋지만, 각 시점에서 ƒ (x) =x와 같은 함수의 변화 속도를 어떻게 찾는가? y 와 같은 방정식과 달리 = mx + b, 함수의 변화 속도 ƒ (x) = x 일정하지 않으며 모든 시점에서 변화하고 있습니다. 이런 종류의 전력 기능의 변화 속도를 어떻게 포착합니까?
선형 방정식의 경우 y (Δy/Δx)의 변화에 대한 x의 변화의 비율을 찾아 방정식의 변화율을 발견했습니다. 함수 ƒ (x) = x 부터 시작하겠습니다 . x에 대해 두 값을 선택하면 ƒ (1) =1 및 ƒ (2) =4. Δy/Δx를 해결하면 (4-1)/(2-1) =4를 얻을 수 있습니다. 이 두 지점 사이를 통과하는 선의 경사는 4입니다. 이제 우리는이 과정을 반복했다고 상상해보십시오. 우리는 x 값이 서로 가까운 x 값을 선택합니다 (1과 1.5). 이것은 우리에게 :
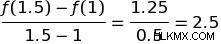
우리가 더 가까워지면 어떻게해야합니까? 1과 1.1은 어떻습니까? 이 값을 막으면 다음과 같이됩니다.
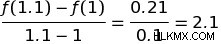
1과 1.01은 어떻습니까? :이것들은 우리에게 :
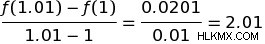
우리의 ΔX가 임의로 작게 성장함에 따라 ΔY/ΔX의 비율은 일부 값에 접근합니다.이 경우 2. 그래픽 용어에서는 X의 더 작고 작은 차이를 계속 선택하면 단일 지점에서 함수의 기울기가 더 가까이 다릅니다. 이것은 결국 우리에게 그 시점에서 기능의 파생물을 줄 것입니다.
그래서 우리는 단일 지점에서 함수의 미분을 근사화하는 방법을 찾았습니다. 함수의 미분은 점에 접근하는 일련의 작고 작은 Δx에 의해 근사 될 수있다. 이것은 우리에게 한계 표기법으로 작성된 값의 파생물을 제공하기위한 일반적인 정의를 제공합니다. 즉,
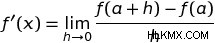
본질적으로,이 방정식은 ƒ (a)의 미분은 H Δy/Δx 비율이 무한하게 작아지는 한계와 같다고 말합니다. h 의 값 그것은 0에 매우 가깝습니다. 그 시점에서 그래프의 기울기에 대한 근사치를 줄 것입니다. 아이디어는 H에 대해 작고 작은 값을 선택함에 따라 기능의 해당 지점에서 탄젠트 라인의 기울기에 가까워지고 가까워집니다. 이것은 파생물의 공식적인 정의이며 미분 기능 를 도출하는 데 사용될 수 있습니다. -즉. 모든 입력 값을 초기 함수의 변화 속도에 따라 한동안 맵핑하는 함수
우리의 기능으로 돌아가 봅시다 ƒ (x) =x 2 . 이 기능을 파생 정의에 연결하면 ƒ (x) =x 2 에 대한 파생 함수를 도출 할 수 있어야합니다. . 그렇게하면 우리에게 다음과 같이됩니다 :
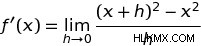
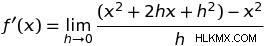
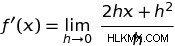
h를 고려하면 우리에게 :
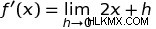
이 방정식에서 h는 실제로, 정말 작은 값으로 간주되므로, 우리는 본질적으로 방정식의 h를 무시하고 다음과 같이 단순화 할 수 있습니다.
.
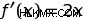
즉, ƒ (x) =x의 미분 함수는 단지 ƒ '(x) =2x입니다. 함수 XAT의 변화 속도는 모든 지점 X는 2x와 같습니다. x =1, ƒ '(1) =2, x =2, ƒ'(2) =4, x =3, ƒ '(3) =6 등. 미분 함수는 입력 값의 변화와 관련하여 각 지점에서 초기 기능의 변화 속도를 제공합니다. 이 그래프의 모든 x 값에 대해 함수는 2x에 비례하는 속도로 변경됩니다.
컴퓨팅 파생 상품에 대한 일반적인 규칙
첫 번째 규칙은 일정한 기능의 미분을 포함합니다. 일정한 출력을 제공하는 모든 함수의 경우 해당 함수의 파생물은 0입니다.
입니다.
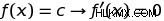
상수 함수는 동일한 출력 만 제공하므로 변경 속도는 항상 0이므로 ƒ (x) =7이면 ƒ '(x) =0.
.다음으로, X의 미분을 어떤 n도 다항식으로 도출하는 이전 과정을 일반화하면, 다항식 용어의 파생물을 찾는 일반적인 규칙 :
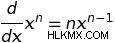
이것을 전력 규칙 이라고합니다 다중 학위 다항식의 유도체를 계산하는 데 사용될 수 있습니다. 전력 규칙을 사용하여 X의 미분이 3X이고 X의 미분이 4 배 이상인지 확인할 수 있습니다.
지수 함수의 경우, 기능 자체에베이스의 자연스러운 로그를 곱하여 미분을 찾을 수 있습니다. 이것은 :
입니다
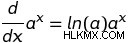
이것을 지수 규칙 이라고합니다 . 지수 규칙은 e의 파생물을 찾기위한 특별 규칙의보다 일반화 된 버전입니다. 모든 함수 중에서 f (x) = e 파생물 자체가 유일한 기능입니다. 즉, 그래프 e 에 접하는 모든 선의 경사 그냥 e. 입니다
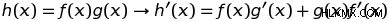
위의 네 가지 표현은 표현의 파생 상품을 찾는 가장 일반적인 규칙입니다. 또한 기능과 파생 상품의 조합을 지배하는 규칙이 있습니다. 예를 들어, 합계 가 있습니다
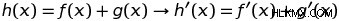
합계 규칙은 일부 함수 h가 두 개의 다른 함수 f와 g의 합인 경우, h의 미분은 f 및 g의 유도체의 합과 같다는 것을 알려줍니다. 합계 규칙을 통해 각 용어의 파생물을 다항식 방정식에서 찾아서 함께 추가하여 총 유도체를 얻을 수 있습니다. 예를 들어 ƒ (x) =x+4x-3x를 상상해보십시오. 합계 규칙은이 함수의 미분이 구성 함수의 파생 상품의 합과 같을 것이므로 ƒ '(x) =3x+8x-3
.다음은 제품 규칙 입니다 기능 제품의 제품의 파생물을 찾기위한 공식을 제공합니다. 제품 규칙은 다음과 같습니다.
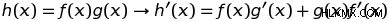
제품 규칙은 두 함수의 생성물의 미분이 첫 번째 함수의 시간과 동일하며, 두 번째 기능은 첫 번째 기능의 시간과 동일하다는 것을 알려줍니다. 따라서 ƒ (x) =sin (x) x의 미분은 ƒ '(x) =sin (x) 2x + xcos (x)입니다. 니모닉“왼쪽 디 오른쪽, 오른쪽 Dee Left”(ldr rdl)
로 제품 규칙 의이 순서를 기억할 수 있습니다.마지막으로 체인 규칙 입니다 기능의 구성의 미분을 설명합니다. 일부 기능이 다른 두 가지의 구성 인 경우, 체인 규칙은 복합 기능의 미분이 g (x)에서 평가 될 때 첫 번째 함수의 미분과 동일하며, g (x)의 미분을 곱합니다. 상징적으로 이것은 :
입니다
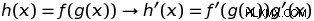
체인 규칙을 통해 기능을 함수 내에 넣고 해당 복합 기능의 파생물을 제공 할 수 있습니다.
이 규칙을 사용하면 대부분의 표준 다항식 방정식의 파생물을 계산할 수 있습니다. 일부 기능은 더 복잡하지만 위의 규칙을 확실하게 적용하면 실제 값 기능의 레이어를 껍질을 벗기려면 파생물을 도출 할 수 있습니다.