지리학자들은 수많은 삼각형을 끌어 들여 고도를 측정합니다. 세면 중 하나는 고도를 측정 해야하는 산의 고도입니다. 이것은 Theodolite로 알려진 고급 분열기를 사용하여 달성됩니다. 그리스인조차도“삼각형의 양면의 비율을 비교하여”고도를 측정했습니다.
오래된 전설에 따르면, 호평을받은 웨일스 어 측량사이자 지리학자 조지 에베레스트 경은 피크 XV라고 알려진 에베레스트 산을 측정 한 후 정확히 29,000 피트 높이로 측정했을 때, 그의 팀은 측정에 2 피트를 추가하여 더 믿을 수있게하기로 결정했습니다. 구름 피어싱 서밋은 해발 29,002 피트에서 침착하게 반복되는 것으로 여겨졌다.

Drukair2에서 본 에베레스트 산 (사진 크레디트 :Shrimpo1967 / Wikimedia Commons)
그 후, 위성과 같은 정교한 기술의 출현은 피크 높이의 높이가 29,029 피트입니다. 그러나 에베레스트 경의 발견은 1852 년에 지리학자들이 현재 장착 된 도구의 도움없이 그것을 만들었다는 것을 고려할 때 매우 주목할 만하다. 또한, 그의 팀은 네팔 정부가 영국인들이 자국에 입국 할 수 없기 때문에 최고점에서 100 마일 이상 떨어진 측정을 수행했습니다. 그래서 그들은 어떻게이 놀라운 업적을 달성 했습니까?
삼각법
어린 시절, 길이를 결정하는 것이 가장 오래된 방법은 내 손으로 확장하는 것이 었습니다. 단일 측정 단위는 손이 적당히 늘어 났을 때 엄지 손가락과 핑키 사이의 거리입니다. 예를 들어 테이블을 측정하기 위해 뻗은 손을 넣을 것입니다. 다음으로, 핑키는 앞으로 뛰어 내려 엄지 손가락을 대신하여 길이를 두 개의 단위를 측정 할 수 있습니다. 맹세는 전체 길이가 설명 될 때까지 계속 될 것입니다.
결국, 손은 통치자로 대체되었지만 방법론은 동일하게 유지되었습니다. 전체 길이가 덮일 때까지 다른 방법 옆에 쌓아 둡니다. 아무도 에베레스트 산이 통치자 또는 손이 가능한지 측정하는 것을 부정하지 않을 것입니다. 그러나 모든 사람이 그 과정이 이라는 데 동의 할 것이라고 확신합니다. 비트 시간이 소요되고 번거 롭습니다.

(사진 크레디트 :Pixabay)
그러나 지리학자들이 의존하는 방법은 통치자를 사용하는 것과 그리 멀지 않습니다. 실제로 에베레스트 경과 그의 팀은 에베레스트 산의 고도를 측정하기 위해 고등학교 기하학을 구현했습니다. 예, 맞습니다. 그들의 도구는 단지 더 멋진 통치자와 통치자 세트였습니다. Trigonometry는 그리스인들에 의해 높은 구조물과 빅토리아 측량사들이 위성으로 이동하기 전에 가장 높은 산을 측정하기 위해 사용되었습니다. 그러나 위성조차도 본질적으로 동일한 원리를 구현하여 고도를 측정합니다.
삼각형
지리학자들은 수많은 삼각형을 끌어 들여 고도를 측정합니다. 세면 중 하나는 고도를 측정 해야하는 산의 고도입니다. 삼각형의 바닥은 산의 발과 포인트 사이에 그려져 있습니다. 세 번째 측면은 간단히 지점 A와 정상 회담을 연결하여 형성 될 수 있습니다.
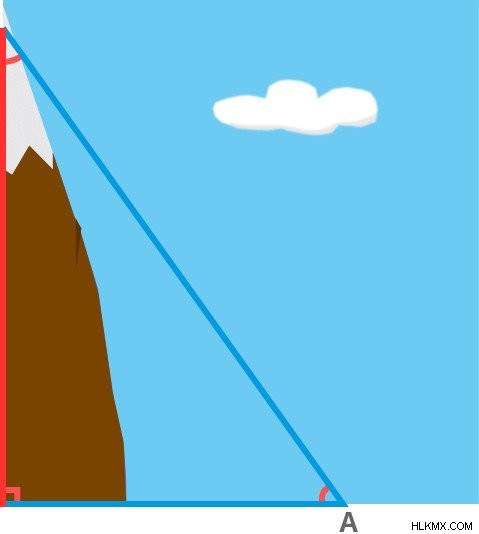
수평 기지를 형성하는 동안 지리학자는 정확한 결과를 얻는 것이 완전히 레벨인지 확인해야합니다. 지구의 울퉁불퉁 한 표면의 불규칙성을 식별하는 것은 매우 섬세한 악기의 도움으로 달성됩니다. 다음으로 삼각형 내에 형성된 세 가지 각도를 모두 측정해야합니다. 이것은 Theodolite로 알려진 고급 분열기를 사용하여 달성됩니다. 삼각형에 의해 제한되는 세 가지 각도의 합의 합은 180º와 같기 때문에, 180에서 알려진 두 각도의 합을 빼면 세 번째 각도를 계산할 수 있으므로 두 각도를 측정하는 것은 충분합니다.
.이제 간단한 트리그의 마법을 보라 - 두 각도에 대한 지식과 한쪽의 길이는 산의 고도를 드러 낼 수 있습니다. 그리스인조차도“삼각형의 양면의 비교를 비교하여 고도를 측정했습니다.
예를 들어, 지점 A에서 형성된 각도가 60º 인 매우 간단한 예제를 고려하고, 우리는 지점 A와 산의 기초 사이의 거리, 즉 삼각형의 기초가 있습니다. 단순화하기 위해 삼각형이 오른쪽의 정각이라고 가정 해 봅시다. 여기서베이스는 고도에 수직입니다. 이것은 정상에서 형성된 세 번째 각도가 30º (180º- [90º+60º])임을 의미합니다. 삼각형의 측면에도 레이블을 지정합시다. 고도에서 시작하여 시계 방향으로 시작하여 x, y 및 z 유닛으로 레이블을 지정하겠습니다.
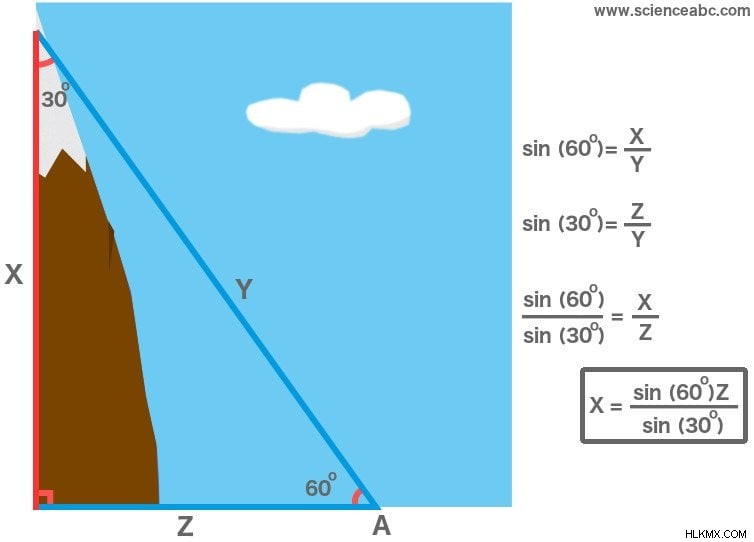
이제 죄 (60º)는 x/y 비율을 나타내고 죄 (30º)는 z/y 비율을 나타냅니다. 이 비율을 나누면 두 ys가 취소되고 x/z 비율 만 남습니다. 죄 (60º)와 죄 (30º)의 가치는 단순히 고등학교 수학 교과서를 언급하여 배울 수 있습니다. 또한 Z는 삼각형의 기초이며, 우리가 이미 알고있는 길이의 크기입니다. Z의 비율에 z를 곱하면 산의 고도 - x -가 있습니다.
에베레스트 경은 하나의 삼각형의 측정을 신뢰할 수 없었기 때문에 다른 A에서 나오는 여러 삼각형을 그렸습니다. 그런 다음 팀은 모든 삼각형에서 파생 된 모든 고도를 평균했습니다. 이로 인해 그들은 29,000 피트 이상에 도착하게되었으며, 숫자는 의심을 막기 위해 증가했다는 소문이 있습니다.
.나중에 1999 년 위성의 도움을받은 과학자들은 에베레스트의 고도를 평균 해수면에서 29, 029 피트로 측정했습니다. 에베레스트 경의 정밀도는 경이로운 것은 아닙니다. 진정한 피크는 그가 예측 한 것보다 27 피트에 불과합니다. 두 각도와 한쪽 만, 그게 다!







