일정한 가속 아래 직선으로의 움직임은 일반적인 물리학 숙제 문제입니다. 관련 조건을 설명하는 동작 방정식과 관련된 문제를 해결하는 데 사용할 수 있습니다. 이 방정식은 다음과 같습니다.
(1) x =x 0 + v 0 t + ½ at
(2) v =v 0 + at
(3) v =v 0 + 2a (x - x 0 )
어디
X는 이동 거리입니다
x 0 초기 시작점입니다
V는 속도입니다
v 0 초기 속도입니다
A는 가속입니다
t는 시간입니다
이 예제 문제는 이러한 방정식을 사용하여 끊임없이 가속되는 몸의 위치, 속도 및 시간을 계산하는 방법을 보여줍니다.
예 :
블록은 2m/s의 일정한 가속으로 마찰이없는 표면을 따라 미끄러 져 들어갑니다. 시간 t =0 s에서 블록은 x =5m이고 3m/s의 속도로 이동합니다.
a) t =2 초의 블록은 어디에 있습니까?
b) 2 초에 블록의 속도는 얼마입니까?
c) 속도가 10m/s 인 블록은 어디에 있습니까?
d)이 시점에 도달하는 데 얼마나 걸렸습니까?
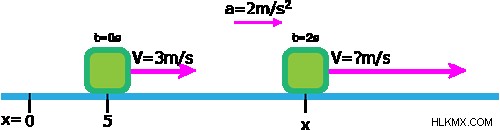
솔루션 :
다음은 설정의 그림입니다.
우리가 아는 변수는 다음과 같습니다.
x 0 =5m
v 0 =3 m/s
a =2 m/s
part a) t =2 초의 블록은 어디에 있습니까?
방정식 1 은이 부분에 유용한 방정식입니다.
x =x 0 + v 0 t + ½at
t로 t =2 초를 대체하고 x 0 의 적절한 값 및 v 0 .
x =5 m + (3 m/s) (2 s) + ½ (2 m/s) (2 s)
x =5 m + 6 m + 4 m
x =15 m
블록은 t =2 초에 15 미터 마크에 있습니다.
파트 b) t =2 초의 블록의 속도는 얼마입니까?
이번에는 식 2가 유용한 방정식입니다.
v =v 0 + at
v =(3 m/s) + (2 m/s) (2 s)
V =3 m/s + 4 m/s
v =7 m/s
블록은 t =2 초에 7m/s로 이동합니다.
Part C) 속도가 10m/s 인 블록은 어디에 있습니까?
방정식 3은 현재 가장 유용합니다.
v =v 0 + 2a (x - x 0 ))
(10 m/s) =(3 m/s) + 2 (2 m/s) (x - 5 m)
100 m/s =9 m/s + 4 m/s (x - 5 m)
91 m/s =4 m/s (x - 5 m)
22.75 m =x - 5 m
27.75 m =x
블록은 27.75m 마크에 있습니다.
part d)이 시점에 도달하는 데 얼마나 걸렸습니까?
당신이 할 수있는 두 가지 방법이 있습니다. 문제의 파트 C에서 계산 한 값을 사용하여 식 1을 사용하고 T를 해결하거나 방정식 2를 사용하여 t를 해결할 수 있습니다. 방정식 2가 더 쉽습니다.
v =v 0 + at
10 m/s =3 m/s + (2 m/s) t
7 m/s =(2 m/s) t
⁄ 2 s =t
⁄ 2 가 필요합니다 27.75m 마크에 도달하려면 S 또는 3.5 초
이 유형의 문제의 까다로운 부분 중 하나는 질문이 요구하는 것에주의를 기울여야한다는 것입니다. 이 경우, 당신은 블록이 얼마나 멀리 여행했는지 묻지 않았지만 그것이 어디에 있는지 묻지 않았습니다. 기준점은 원점에서 5 미터입니다. 블록이 얼마나 멀리 여행했는지 알아야한다면 5 미터를 빼야합니다.
추가 도움을 얻으려면 이러한 모션 예제 예제 문제를 시도하십시오.
운동 방정식 - 차단 예
운동 방정식 - 수직 운동
운동 방정식 - 차량 차량
운동 방정식 - 발사체 운동