Atwood Machine은 지속적인 가속을 겪고있는 두 개의 결합 시스템의 운동 법칙을 보여주는 일반적인 교실 실험입니다. Atwood 기계는 두 가지 질량 M a 로 구성됩니다 및 m b , 질량이없는 풀리 위에 부적절한 질량이없는 끈으로 함께 결합합니다. 두 질량이 동일하면 시스템은 평형 상태이며 움직임이 발생하지 않습니다. 두 질량은 고정 상태로 유지됩니다. 두 무게가 같지 않으면 시스템은 더 가벼운 질량을 끌어 당기는 동안 더 무거운 질량이 뽑히는 곳으로 이동합니다. 이 예제 문제는 시스템의 가속도와 문자열의 장력을 도출하는 방법을 보여줍니다.
문제 :
a) m a 인 경우 Atwood 기계의 가속도를 찾으십시오. =3 kg 및 m b =5 kg.
b) 두 질량을 연결하는 줄의 장력을 찾으십시오.
다음은 설정의 그림입니다.
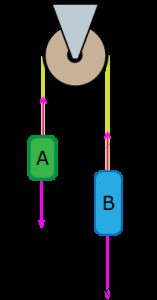
우리는 m a 의 값을 무시할 것입니다 및 m b 이 시점에서 답의 파생을 보여줍니다. 블록 B는 블록 A보다 무겁기 때문에 전체 모션 방향은 풀리의 블록 B 측면과 블록 A의 측면에서 아래로 내려갑니다. 가속도가 항상 긍정적이어서 좌표계를 선택하십시오.
이 시스템은 Massless String으로 함께 연결됩니다. 더 무거운 블록 B는 스트링에서 거리에서 Δd를 찢어집니다. 동시에, 블록 A는 ΔD로 이동합니다. 즉, 각 블록의 속도가 동일하다는 것을 의미합니다.
v a =⁄ t =v b
속도 방향은 각 시스템에 대해 선택한 좌표계에 의해 조정될 수 있습니다. 속도는 항상 동일하기 때문에 가속도는 동일합니다.
a =a a =a b
문자열은 질량이없고 rectensable이므로 시스템 전체에서 장력이 균일합니다. 장력 당기기 블록 A를 업무를 당기는 것은 장력을 당기는 블록 B Up과 동일합니다.
이것은 가속도와 장력이 두 블록 모두에 대해 동일하다는 것을 의미합니다. 이제 각 블록에서 작용하는 힘을 찾으십시오.
블록 a의 경우, 가중치 m a 장력 T가 위로 올라가는 동안 g가 당겨지고 있습니다.
σf =t - m a g
이 힘이 움직이고 있기 때문에,이 힘은 m a 와 같습니다. a.
σf =m a a =t - m a g
블록 B의 경우 힘은 거의 동일합니다. 차이점은 전체 가속도가 블록 a의 반대 방향에 있다는 것입니다.
σf =m b g - t =m b a
우리는 이제 두 개의 방정식과 두 개의 미지의 T와 a를 가지고 있습니다. 이 두 방정식을 함께 추가하면 T가 가속 만 남기지 않습니다.
m a a =t - m a g
m b a =-t + m b g
m a a + m b a =m b g - m a g
양쪽의 가속도 및 중력 변수를 고려하십시오.
(m a + m b ) a =(m b - m a ) G
양쪽을 (m a 로 나눕니다 + m b ) a.


가속도가 있기 때문에이 두 힘 방정식 중 하나를 사용하여 장력을 찾는 데 사용할 수 있습니다. 블록 a.
를 사용합시다m a a =t - m a g
이것을 t에 대해 해결하고 얻으십시오 :
t =m a a + m a g
가속도 (a) 공식을 방정식으로 대체하십시오.

방정식을 다시 작성하십시오

m a 을 고려하십시오 g

괄호 안에 공통 분모가 있도록 1을 변경하십시오.

두 개의 분수를 함께 추가하여 얻을 수 있습니다

간단하게 얻습니다

그게됩니다

초기 문제에 대한 답을 찾으려면이 공식을 사용하여 가속 및 장력을 사용하십시오.
파트 A) m a 일 때 가속도를 찾으십시오 =3 kg 및 m b =5 kg.
앞서, 우리는 가속도가
임을 알았습니다

m a 의 값을 입력하십시오 및 m b .
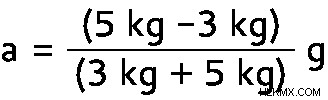
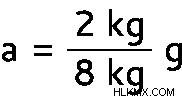
a =2/8 g
a =0.25 (9.8 m/s)
a =2.54 m/s
블록은 2.54m/s에서 가속합니다.
파트 B) 문자열에서 장력을 찾으십시오.




t =36.75 kg · m/s
KG · M/S는 뉴턴 힘의 유닛과 동일합니다.
t =36.75 n
문자열의 장력은 36.75 Newtons입니다.
팁 :
이러한 유형의 문제의 핵심은 가속의 방향이 항상 긍정적 인 방향에 있도록 좌표계를 선택하는 것입니다. 가속화가 모두 함께 행동하는 한 부호 오류는 문제가되지 않습니다. Atwood 기계의 경우 가속도는 항상 더 큰 질량을 향해 달려갑니다.