높이와 거리에서 문제를 해결했습니다

물리학의 높이와 거리 주제는 엄청난 중요성을 가지고 있습니다. 이 주제는 경쟁 시험에서 중요합니다. 높이와 거리에서 해결 된 문제의 도움으로 더 잘 이해할 수 있습니다. 이 주제의 문제는 일반적으로 건물 높이 측정을 중심으로 진행됩니다. 또한 한 건물의 높이와 고도 또는 우울증 각도가 표시되면 다른 건물의 높이를 찾는 것도 포함될 수 있습니다. 또 다른 형태는이 두 건물 사이의 거리를 찾는 것입니다. 높이와 거리에서 이러한 해결 된 문제로부터 혜택을 받기 위해 계속 읽으십시오.

높이와 거리에 대한 문제 해결 :관련 항

높이와 거리에 대한 해결 된 문제를 탐구하기 전에 먼저 관련 용어에 익숙해 져야합니다.

고도 각도 :개인이 땅에 서 있다고 가정합니다. 이 개인의 시력은 건물 꼭대기에있는 물건에 있습니다. 여기서 시야는 건물의 정상과 개인의 눈을 연결하는 선입니다. 가장 중요한 것은 고도 각도는 수평선으로 시야에 의해 생성 된 각도입니다.

우울증의 각도 :개인이 볼 수있는 물체의 어느 정도 높이에 서 있다고 가정합니다. 여기서 시야는 건물의 바닥과 개인의 눈을 연결하는 선입니다. 가장 중요한 것은 우울증의 각도는 수평선으로 시야에 의해 생성 된 각도입니다.

이 용어는 높이와 거리에 대한 해결 된 문제를 연구함으로써 당신에게 더 명확해질 것입니다.

높이와 거리에 대한 문제 해결 :예 :

높이와 거리의 해결 된 문제를 살펴 보겠습니다 :

1. 80m 높이의 등대 정상에서 누군가가 두 배를 관찰합니다. 이 등대 상단에서 관찰되는이 선박의 고도 각도는 각각 45 °와 30 °로 나옵니다. 이제 관찰되는 두 선박 사이의 거리를 측정합니까?

솔루션 :

여기, AB 또는 H가 80m이고 등대입니다.

또한, 선박이 지점 P와 Q에있는 것을 고려하십시오.

Δbap에서 tan 45 ° =ba/bp

따라서 1 =80/bp

따라서 bp 또는 x =80m

따라서 bq =80 + pq

ΔBaq에서, tan30 ° =ba/bq

따라서, 1/√3 =80/(80+pq)

또한, (80+pq) =80√3

마지막으로, 우리는 pq =80 (√3-1) =80 x 0.732 =58.56m

따라서 등대 상단에서 관찰 된 선박 사이의 거리는 58.56m입니다.

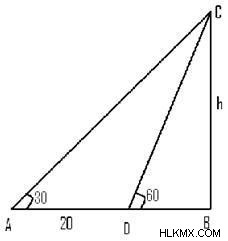
2. 건물 상단의 고도는 60 ° 인 것으로 밝혀졌습니다. 이 건물은 수평 평면의 발에서 측정 될 때 50m 거리에 있습니다. 이제 건물의 높이를 계산합니까?

여기서는 건물의 높이는 AC.

BC는 건물과 관찰 지점 사이의 거리를 보여줍니다.

이제 오른쪽 삼각형 ACB를 고려하십시오 :

여기, 측면 AC는 고도 각도와 반대되는 쪽입니다.

또한 hypotenuse side ab는 90 °와 반대되는 쪽입니다. 또한, 인접한 BC는 나머지 측면입니다.

이제 위의 매개 변수가 주어지면 측면 AB의 길이를 계산해야합니다.

tanθ =반대쪽/인접한 쪽. 이것은 우리에게 tan60 ° =ac/bc

또한 √3 =ac/50

또한, √3 x 50 =ab

ac =50√3

√3의 대략적인 값은 1.732

그래서 우리는 ac =50 (1.732)

마지막으로, 우리는 ac =86.6 m

그래서 건물의 높이는 86.6m입니다.

높이 및 거리 질문에 대한 문제를 해결했습니다

아래 키와 거리 질문에 대한 해결 된 문제를 살펴 보겠습니다.

1. 레벨 그라운드에서는 30 ° 상승 각도가 탑의 상단과 함께 형성됩니다. 이제 타워를 향해 20 미터로 이동하면 45 °의 고도 각도가 형성됩니다. 4 가지 옵션 중 탑의 높이는 얼마입니까?

1. - 10√3

2. - √3

3. - 10

4. - 20√3

정답 :a

설명 :

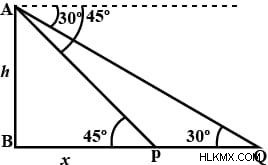
탑의 높이가 h

그러한 상황에서는 20 =h (cot30 - cot60)

또한 20 =h (√3 - 1/√3)

또한 20√3 =h (3-1)

마지막으로, 우리는 h =10√3

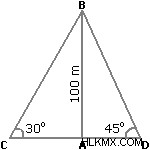
2. 특정 등대의 양면에 항해하는 두 배가 있습니다. 선박과 등대 상단에서 관찰 된 바와 같이 고도 각도는 각각 30 °와 45 °입니다. 이제 등대의 높이가 100m라고 가정하십시오. 아래에 주어진 4 가지 옵션 중 두 선박 사이의 거리는 얼마입니까?

a. 173 m

b. 200 m

c. 300 m

d. 273 m

정답 :d

설명 :

등대를 AB.

또한 선박 위치가 C와 D라고 가정하자

그러한 상황에서는 다음과 같은 것을 가질 것입니다.

ab =100 m

ξACB =30 °

ξadb =45 °

ab/ac =tan 30 ° =1/√3

이것은 우리에게 ac =ab x √3 =100/√3

이제

ab/ad =tan 45 ° =1

이것은 우리에게 줄 것입니다

ad =ab =100m

따라서 cd =ac + ad

so, ac + ad =100/√3 + 100m

마지막으로, 우리는 cd =273 m.

결론

높이와 거리 주제는 물리학의 중요한 구성 요소입니다. 물리학 장을 연구하면 어떤 식 으로든 높이와 거리를 다룰 가능성이 있습니다. 높이와 거리에 대한 해결 된 문제는이 주제를 마스터하기위한 필수품입니다. 고도의 각도와 우울증 각도는이 주제와 관련된 두 가지 관련 용어입니다. 마지막으로, 철저한 이해를 위해 높이와 거리 예와 질문에 대한 해결 된 문제를 연구하십시오.

• 
  엔진이 실패하면 비행기가 어떻게 비행 할 수 있습니까? 읽은
• 
  시간에 대해 알고있는 모든 것을 잊어 버리십시오 읽은
• 
  새로운 웜홀을 통해 정보는 블랙홀을 피할 수 있습니다 읽은
• 
  전위 쌍극자 읽은