상대 각속도

각속도는 무엇입니까?

각속도는 시간 내 각도 위치의 변화 속도로 정의 될 수 있습니다. 벡터 수량입니다. 그것의 방향은 위치 벡터와 속도의 방향에 수직입니다.

벡터 분석에서, 우리는 벡터 수량 a의 변화 속도가 일정한 각도 속도 ω가있는 지점 주위에 회전 될 때,

da/dt =ω x a

따라서 포인트에 대한 위치 벡터 r의 변화율은

 dr/dt =ω x r

⇒ v =ω x r

v 여기에 그 지점에 대한 속도가 있습니다. 이것은 각속도와 속도 벡터 사이의 표준 관계입니다. 위치 벡터와 각속 속도의 방향이 상호 직각 인 경우 위의 방정식을 V =ωr로 쓸 수 있습니다. 여기서이 경우 기준점은 휴식 중입니다.

각속도는 시간의 각도 변화 속도로 정의 될 수 있습니다.

ω =dφ/dt

상대 속도 :

신체의 상대 속도는 움직이는 다른 신체의 기준 프레임에서 신체의 속도로 정의 될 수 있습니다. B와 함께 각도 φ로 이동하는 신체 B에 대한 신체 A의 상대적 속도는

vab =(va2 + vb2-2vavbcosφ) ½

단단한 몸의 회전에서 상대 각속도.

회전 축에 대한 강성 몸의 점의 각속도는 항상 강체의 각속도와 동일합니다. 그러나 우리가 회전 축에서 참조 지점을 빼면, 그 강체의 점의 상대적 각속도는 우리가 선택한 지점에 따라 변할 것입니다.

예를 들어, 아래 그림에 표시된 디스크의 회전을 살펴 보겠습니다.

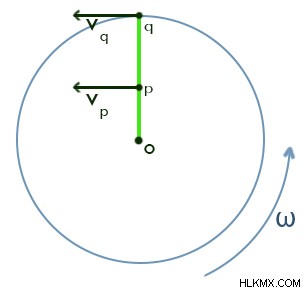여기서 우리는 디스크에서 두 가지 점을 고려했습니다. 두 지점을 p와 ​​q라고합니다. 여기서 디스크는 각속도 ω로 회전합니다. 따라서 점 P와 Q의 각속도는

vp =ωrp (rp와 rq는 각각 중심에서 p와 q의 거리입니다.)

여기서 우리는 p에 대한 점 Q의 상대 각도 속도를 찾아야합니다. 따라서 p에 대한 Q의 각속도를 ωqp로 작성하십시오. 따라서 ωqp는

ωqp =(vqp의 수직 성분) / (rq-rp), (vqp =p와 q 사이의 상대 속도)

따라서, ωqp =(vq-vp)/(rq-rp)

⇒ ωqp =(ωrq-ωrp)/(rq-rp)

⇒ ωqp =ω

이것은 두 지점 사이의 상대 속도의 값입니다. 값은 두 지점 사이의 거리와 무관하므로 ωqp =ω가 해당 디스크의 두 지점 사이의 상대 각속도가 될 것이라고 말할 수 있습니다.

또한, 우리는이 분석을 사용하여 강체의 두 지점 사이의 상대 각속도의 값이 그 신체의 회전의 각속도와 같을 것이라고 주장 할 수 있습니다.

우리는 또한 상대 속도가 원하는 참조 프레임과 관련하여 위치 벡터의 변화 속도라고 말할 수 있습니다. 

참고 :우리는 여기에 간단한 형태가되도록 상대 속도를 얻었지만 더 큰 계산을 위해 상대 각속도에 대한 표현이 더 복잡해집니다. 

두 몸 사이의 상대 각속도는 다른 각도와 함께 움직입니다.

아래 그림과 같이 속도 VX와 VY에서 각각 움직이는 두 바디 x와 y를 고려해 봅시다.

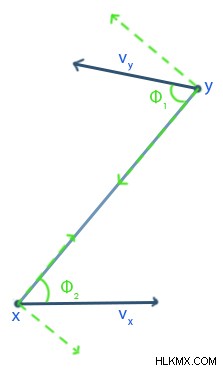
여기서 x와 y 사이의 상대 속도의 수직 구성 요소를 찾아야합니다.

두 바디를 결합하고 두 바디를 결합하는 선과 평행 한 선에 수직 인 속도 벡터를 해결할 때, 우리는 상대 속도의 수직 구성 요소가

vxy v =vysinφ1 + vxsinφ2

따라서 두 몸 사이의 상대적 각속도는

ωxy =vxy 丄 / rxy

⇒ ωxy =(vysinφ1 + vxsinφ2) / rxy

참고 :두 지점과 상대 각속도 사이의 각도 변화 속도 사이에는 차이가 있습니다. 비록 동일하게 보일 수 있지만, 두 지점 사이의 각도 변화 속도는 단순히 다른 지점에 대한 한 지점의 회전 속도를 지배하는 각도 속도와 상대 각도 속도의 차이입니다.

결론 :

두 지점 사이의 상대 각속도는 다른 점에 대한 한 지점의 회전 속도입니다. 이 값은 항상 각각의 각도 속도의 차이와 같지는 않습니다. 강체의 두 지점 사이의 상대 각속도는 강체의 각속도와 동일합니다. 무작위 각도로 움직이는 두 랜덤 바디 사이의 상대 속도는 분리와 상대 방향에 따라 다릅니다. 우리는 항상 상대 각속도를 찾기 위해 상대 속도의 수직 성분을 찾습니다.