방사형 가속

방사상 가속의 주요 적용은 물체 이동, 속도 및 방향 측면에서입니다. 이러한 모든 발생은 서로 관련하여 평가됩니다. 주어진 시간에 물체의 변화 속도는 가속도로 특성화 될 수 있습니다. 가속도는 그 자체 내에서 크기와 방향을 모두 갖는 벡터 수량입니다.

움직임중인 물체의 속도가 변경 될 수 있습니다. 가속도는 시간과 관련하여 차량 속도와 방향의 변화 속도에 대한 측정 단위입니다. 물체의 움직임은 선형 또는 원형 일 수 있습니다. 결과적으로 선형 가속도는 선형 운동과 관련된 가속도에 주어진 이름입니다. 각속도는 원형 운동에 관여하는 가속도입니다.

방사형 가속도

뉴턴의 움직임 법칙에 따르면, 움직이는 물체 나 몸이 움직일 때 속도가 바뀌는 경향이 있으며, 이는 물체에 주어진 힘의 양에 따라 다릅니다.

결과적으로 가속은 방향뿐만 아니라 방향과 시간에 따라 물체 속도의 변화 속도로 정의됩니다. 그러나 물체의 움직임은 선형 또는 원형 일 수 있습니다.

객체의 방사형 가속도는 중심을 향한 가속도로 정의됩니다. 이 가속도는 균일 한 원형 운동으로 발생하며 물체의 반경을 따라 이동하는 것과 관련이 있습니다.

방사상 가속도 단위

방사상 가속도는 초당의 라디안으로 표현되며, 이는 RAD S-2로 작성됩니다.

방사형 가속도 방정식

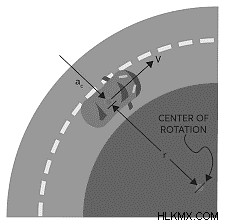
가속도는 크기 또는 방향 또는 둘 다의 속도의 변화입니다. 속도의 양이 균일 한 원형 운동에서 일정 할 수 있더라도 속도의 방향은 지속적으로 변하므로 항상 관련 가속도가 있습니다. 차 안에서 모퉁이를 돌리면이 가속도를 느낍니다. (회전 중에 휠을 안정적으로 유지하고 일관된 속도로 운전하면 균일 한 원형 움직임입니다.) 당신과 자동차가 방향을 바꾸고 있기 때문에, 당신은 옆으로 가속을 인식합니다. 곡선이 더 선명 해지고 속도가 증가함에 따라이 가속도가 눈에 띄게됩니다. 이 섹션에서 그 가속도의 크기와 방향을 살펴 보겠습니다.

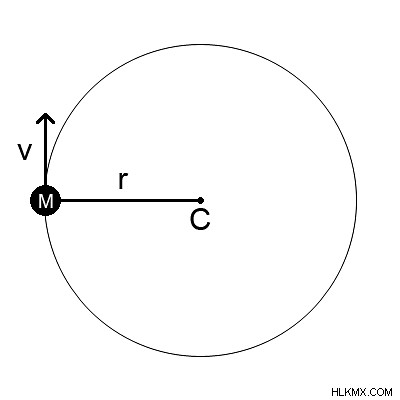
객체 m은 위의 다이어그램의 문자열에 부착 된 다음 원의 중심 인 'c'지점 주위의 고정 축을 회전하도록 만들어집니다. 물체가 빨리 회전하면 문자열 cm은 원의 반경 인 것처럼 보입니다. 가속도 A0은 방사형 방향을 따라 작용합니다.

이 힘에 대응하기 위해, 장력은 문자열을 따라 반대 방향으로 생성됩니다. 중심력은 긴장의 결과로 발생하는 힘입니다. 방사상 가속도 또는 중심 가속도는 신체에 생성 된 가속입니다.

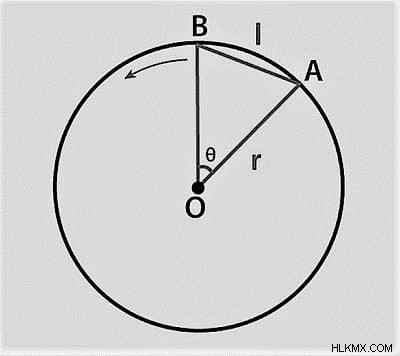
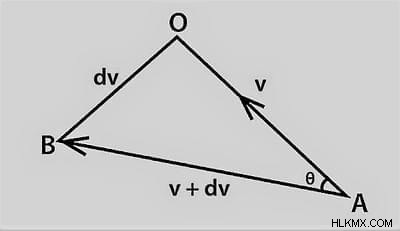
무한하게 서로 더 가깝고 중심 속도 벡터가있는 동등한 삼각형의 정확한 다이어그램이 위의 다이어그램에 표시됩니다.

비슷한 삼각형의 속성이 적용되면

aboa =ir

위치 a와 b가 무한대가 가까우므로 AB에 대한 AB는 AB의 길이로 가정 될 수 있습니다.

ab =v × dt

지점 a와 b가 너무 가깝기 때문에

v+dv≈dv × aboa

dvvvxdtr

dvv

이제 재배치 측면에서

dvdt =v2r

결과적으로 DV / DT는 균일 한 원형 운동으로 항목의 방사형 가속도를 나타냅니다. 결과적으로, 위에서 언급 한 증거의 최종 방정식은 다음과 같습니다.

ar =v2r

방사상 가속도의 크기를 찾는 방법

매번 방사형 가속의 크기는 V2R과 동일합니다. 여기서 v는 속도이고 R은 그 당시 곡률의 반경입니다. 반경은 원형 운동에서 r이며, 방사상 가속 방향은 곡률의 반경을 따라 있습니다.

결론

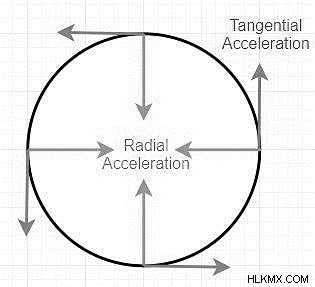
중심 가속도는 신체가 원형 운동의 중심을 향해 움직일 때 경험하는 가속입니다. 이것은 두 부분으로 나눌 수 있습니다. 운동 유형에 따라 방사형 및 접선 구성 요소가 있습니다.

• 방사형 및 접선 가속도는 두 가지 유형의 각도 가속도입니다.

• 객체의 방사형 가속도는 중심을 향한 가속도로 정의됩니다.

• 2 초당의 라디안, RAD S-2로 약칭 된 방사형 가속도 측정 단위입니다.

• 반경 가속도는 중심 가속도의 또 다른 이름입니다.

• 접선 가속도는 원형 경로에 수직 인 각 가속도의 구성 요소입니다.