논리 게이트는 기본적인 수학적 논리 작업을 수행 할 수있는 간단한 디지털 회로입니다. 디지털 전자 장치에는 주로 7 개의 기본 문이 있습니다. 그것들은
입니다 일반적 으로이 게이트에는 여러 입력과 단일 출력이 있습니다. 이러한 다른 게이트를 사용하여 디지털 전자 회로를 구축 할 수 있습니다. 이 기사에서는 2 및 3 입력 Xnor 게이트의 상징, 작업, 진실 표를 연구합니다.
독점 또는 게이트는 게이트가 아닌 XOR 게이트의 간단한 조합입니다. 아래 다이어그램과 같이 2 입력 Xnor 게이트를 고려해 봅시다 :
두 입력은 각각 문자 p와 q로 표시됩니다. 단일 출력은 문자‘Y’로 표시됩니다.
xnor 게이트의 출력은 아래에 주어진 표현에 따라 입력 A 및 B와 관련이 있습니다.
∴ y =(p.q+p.q) …… .. (1)
기호는 '독점 추가'라는 수학적으로 논리 게이트 작업을 나타냅니다.
p와 q는‘높음 (1)’또는‘낮은 (0) 값 만 가질 수있는 이진 입력입니다.
| p
| Q
| y
|
| | 0
|
|
| |
| 0
|
| | 0
| 0
|
| |
|
|
두 입력은 개별적으로“1”또는“0”의 두 가지 가능한 값만을 가질 수 있습니다. 이에 따라 입력에 대한 4 가지 가능한 조합이 있으며 4 개의 다른 출력을 읽을 수 있습니다.
사례 1 - p =0, q =0, 출력 y =1
방정식 (1),
에서 p, q, y의 값을 대체하여 이것을 확인할 수 있습니다. ∴ y =(p.q+p.q) =(0.0+0.0) =(0.1+1.0) =0 =1
사례 2 - p =0, q =1, 출력 y =0
∴ y =(p.q+p.q) =(0.1+0.1) =(0.0+1.1) =1 =0
사례 3 - p =1, q =0, 출력 y =0
∴ y =(p.q+p.q) =(1.0+1.0) =(1.0+0.0) =1 =0
사례 4 - p =1, q =1 인 경우 출력 y =0
∴ y =(p.q+p.q) =(1.1+1.1) =(1.0+0.1) =0 =1
이들은 Xnor 게이트 작업의 네 가지 사례입니다.
구조 -
xnor 게이트는 GATE 및 NAND GATE를 사용하여 구성 할 수 있습니다. 이 두 문은 보편적입니다. 우리는이 두 가지를 사용하여 다른 게이트를 구성 할 수 있습니다.
그림 1 및 그림 2는 각각 NAND 및 NOR 게이트를 사용하여 Xnor 게이트의 구성을 보여줍니다.
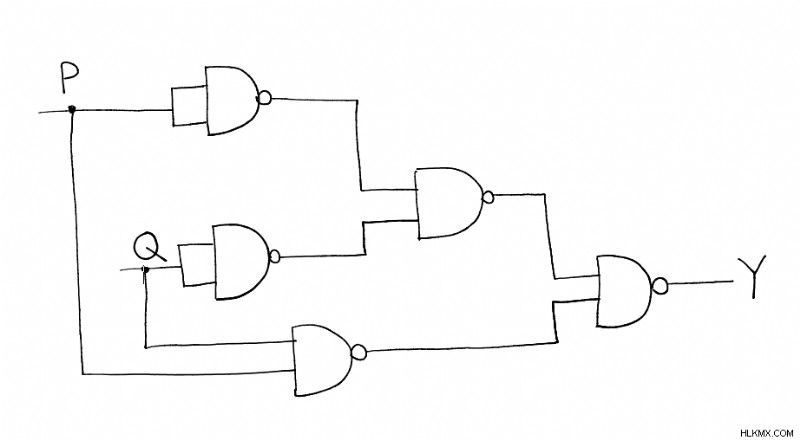 fig.1 xnor gate nand gate를 사용합니다
fig.1 xnor gate nand gate를 사용합니다 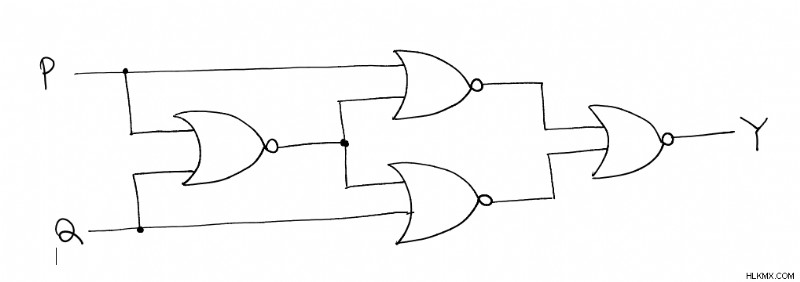
그림 2 xnor 게이트 사용 또는 게이트
3 개의 입력 XNOR 게이트 -
우리는 진실 테이블과 2 입력 Xnor 게이트의 작동을 보았습니다. 이 섹션에서는 3 입력 Xnor 게이트의 작업 및 진실 테이블을 연구합니다.
논리적 표현 -
y =pqr
∴ y =(pq+pq) r
3 입력 xnor 게이트는 3 개의 입력, 즉 p, q 및 r, 1 개의 출력 y.
에 3 개의 입력이 있습니다. 진실 테이블은 다음과 같습니다 -
| Q
| r
| y
|
| | 0
| 0
|
|
| | 0
|
| 0
|
| |
| 0
| 0
|
| |
|
|
|
| | 0
| 0
| 0
|
| | 0
|
|
|
| |
| 0
|
|
| |
|
| 0
|
각 입력은 (1) 또는 낮은 (0) 상태를 가질 수 있습니다. 따라서, 3 개의 입력의 8 가지 다른 조합이있다. 따라서 입력 조합에 해당하는 8 개의 다른 출력을 얻습니다. 입력 및 출력 조합의 가능한 경우를 보자.
사례 1 - p =0, q =0, r =0, 출력 y =1
y =(pq) r =(p.q+p.q) r =(0.0+0.0) 0
∴ y =00 =1
사례 2 - p =0, q =0, r =1, 출력 y =0
y =(pq) r =(0.0+0.0) 1 =(0.0+0.0) 1
∴ y =01 =0
사례 3 - p =0, q =1, r =0, 출력 y =0
y =(pq) r =(0.1+0.1) 0 =(0.0+1.1) 0
∴ y =10 =0
사례 4 - p =0, q =1, r =1, 출력 y =1
y =(pq) r =(0.1+0.1) 1 =(0.0+1.1) 1
∴ y =11 =1
사례 5 - p =1, q =0, r =0, 출력 y =0
y =(pq) r =(1.0+1.0) 0 =(1.1+0.0) 0
∴ y =10 =0
사례 6 - p =1, q =0, r =1, 출력 y =1
y =(pq) r =(1.0+1.0) 1 =(1.1+0.0) 1
∴ y =11 =1
사례 7 - p =1, q =1, r =0, 출력 y =1
y =(pq) r =(1.1+1.1) 0 =(1.0+0.1) 0
∴ y =00 =1
사례 8 - p =1, q =1, r =1, 출력 y =0
y =(pq) r =(1.1+1.1) 1 =(1.0+0.1) 1
∴ y =01 =0
3 입력 xnor 게이트의 8 가지 사례입니다.
Xnor IC -
-
IC 4077
-
IC 74266
결론 -
xnor는 파생 게이트입니다. 게이트가 아닌 XOR의 조합입니다. 이 기사에서는 진실 테이블 및 작업과 함께 2 입력 및 3 입력 Xnor 게이트를 보았습니다. Xnor는 절반 가산기와 전체 가산기 회로를 구성하는 데 널리 사용됩니다.
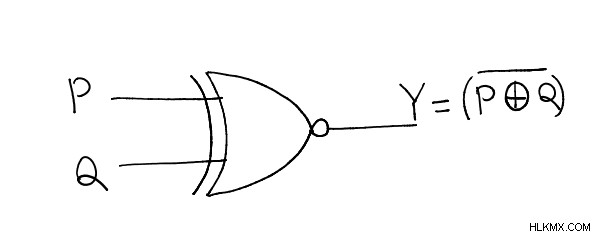
 fig.1 xnor gate nand gate를 사용합니다
fig.1 xnor gate nand gate를 사용합니다